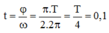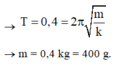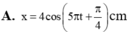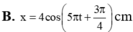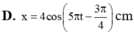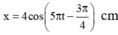Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Khoảng thời gian ngắn nhất giữa hai lần động năng bằng thế năng:
∆ t = T 4 = π 10 ⇒ T = 2 π 5 ( s ) ⇒ ω = 5 ( r a d / s )
Vị trí động năng bằng thế năng( W d = W t )
![]()
Tại vị trí đó, gia tốc có độ lớn 2 m/ s 2 nên
![]()
Cơ năng của vật: W = 1 2 m ω 2 A 2 = 1 2 0 , 25 . 5 2 . ( 0 , 08 2 ) 2 = 0 , 04 J = 40 m J

Chọn đáp án A
Δ t = 60.2 π l g = 50.2 π l + 0 , 44 g ⇒ 6 5 = l + 0 , 44 l ⇒ l = 1 m .

Khoảng thời gian ngắn nhất giữa hai lần liên tiếp vật vật đi qua vị trí có li độ
![]()
+ Lực kéo cực đại của lò xo tác dụng và điểm có định là
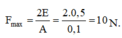
+ Vậy khoảng thời gian ngắn nhất để lò xo kéo điểm cố định một lực 5 N là
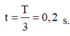
Đáp án D

Đáp án D
Tần số dao động của vật ω = 2 π T = 5 π r a d / s
Vị trí động năng bằng thế năng x = ± 2 2 A , vật chuyển động nhanh dần đều theo chiều dương, ứng với chuyển động từ biên âm về vị trí cân bằng. Do đó x 0 = − 2 2 A → φ 0 = − 3 π 4 rad.
Phương trình dao động của vật x = 4 cos 5 π t − 3 π 4 cm

1) \(W_đ=W_t\Rightarrow W=W_đ+W_t=2W_t\)
\(\Rightarrow \dfrac{1}{2}kA^2=2.\dfrac{1}{2}kx^2\)
\(\Rightarrow x = \pm\dfrac{A}{\sqrt 2}\)
Như vậy, trong 1 chu kì có 4 lần động năng bằng thế năng được biểu diễn bằng véc tơ quay như sau.
x A -A O M N P Q
Đó là các vị trí ứng với véc tơ quay đi qua M, N, P, Q
Như vậy, thời gian giữa 2 lần liên tiếp động năng bằng thế năng là 1/4T
\(\Rightarrow \dfrac{T}{4}=0,2\Rightarrow T = 0,8s\)
\(W_đ=nW_t\)
\(\Rightarrow W = W_đ+W_t=nW_t+W_t=(n+1)W_t\)
\(\Rightarrow \dfrac{1}{2}kA^2=(n+1).\dfrac{1}{2}kx^2\)
\(\Rightarrow \dfrac{A}{x}=\pm\sqrt{n+1}\)
\(\Rightarrow \dfrac{\omega^2. A}{-\omega^2.x}=\pm\sqrt{n+1}\)
\(\Rightarrow \dfrac{a_{max}}{a}=\pm\sqrt{n+1}\)

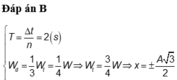
Thời gian ngắn nhất = A 3 2 n ê n x = A 3 2 l à T 3 = 2 3 s

Đáp án A
Wđ = Wt ® Vật ở vị trí
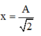
Khoảng thời gian giữa 2 lần liên tiếp