Ai giúp em câu 5 được không ạ em cảm ơn!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LM
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
0
NR
Giúp em 7 8 10 được không ạ em cảm ơn
1
27 tháng 8 2021
10: Ta có: \(\left(\dfrac{x+1}{x}\right)^2:\left[\dfrac{x^2+1}{x^2}+\dfrac{2}{x+1}\cdot\left(\dfrac{1}{x+1}+1\right)\right]\)
\(=\dfrac{\left(x+1\right)^2}{x^2}:\left(\dfrac{x^2+1}{x^2}+\dfrac{2\cdot\left(x+2\right)}{\left(x+1\right)^2}\right)\)
\(=\dfrac{\left(x+1\right)^2}{x^2}:\dfrac{\left(x^2+1\right)\left(x^2+2x+1\right)+2x^2\left(x+2\right)}{x^2\left(x+1\right)^2}\)
\(=\dfrac{\left(x+1\right)^2}{x^2}\cdot\dfrac{x^2\left(x+1\right)^2}{x^4+2x^3+x^2+x^2+2x+1+2x^3+4x^2}\)
\(=\dfrac{\left(x+1\right)^4}{x^4+4x^3+6x^2+2x+1}\)
NL
2
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 1
a.
Ta có \(BD||AC\) (cùng vuông góc AB)
Áp dụng định lý Talet trong tam giác ACE: \(\dfrac{BE}{BA}=\dfrac{DE}{DC}\)
b.
Ta có \(IK||BD||AC\) \(\Rightarrow EI||AC\)
Áp dụng Talet: \(\dfrac{DC}{ED}=\dfrac{DA}{ID}\Rightarrow\dfrac{DC}{DC+ED}=\dfrac{DA}{DA+ID}\Rightarrow\dfrac{DC}{CE}=\dfrac{DA}{AI}\) (1)
Do \(BD||EK\), áp dụng Talet trong tam giác CEK: \(\dfrac{BD}{EK}=\dfrac{CD}{CE}\) (2)
Do \(BD||EI\), áp dụng Talet trong tam giác AEI: \(\dfrac{BD}{EI}=\dfrac{AD}{AI}\) (3)
Từ(1);(2);(3) \(\Rightarrow\dfrac{BD}{EK}=\dfrac{BD}{EI}\Rightarrow EK=EI\)
TM
1
11 tháng 12 2021
Câu 5:
a: Xét tứ giác AHMK có
\(\widehat{AHM}=\widehat{AKM}=\widehat{KAH}=90^0\)
Do đó: AHMK là hình chữ nhật
VT
5
22 tháng 10 2021
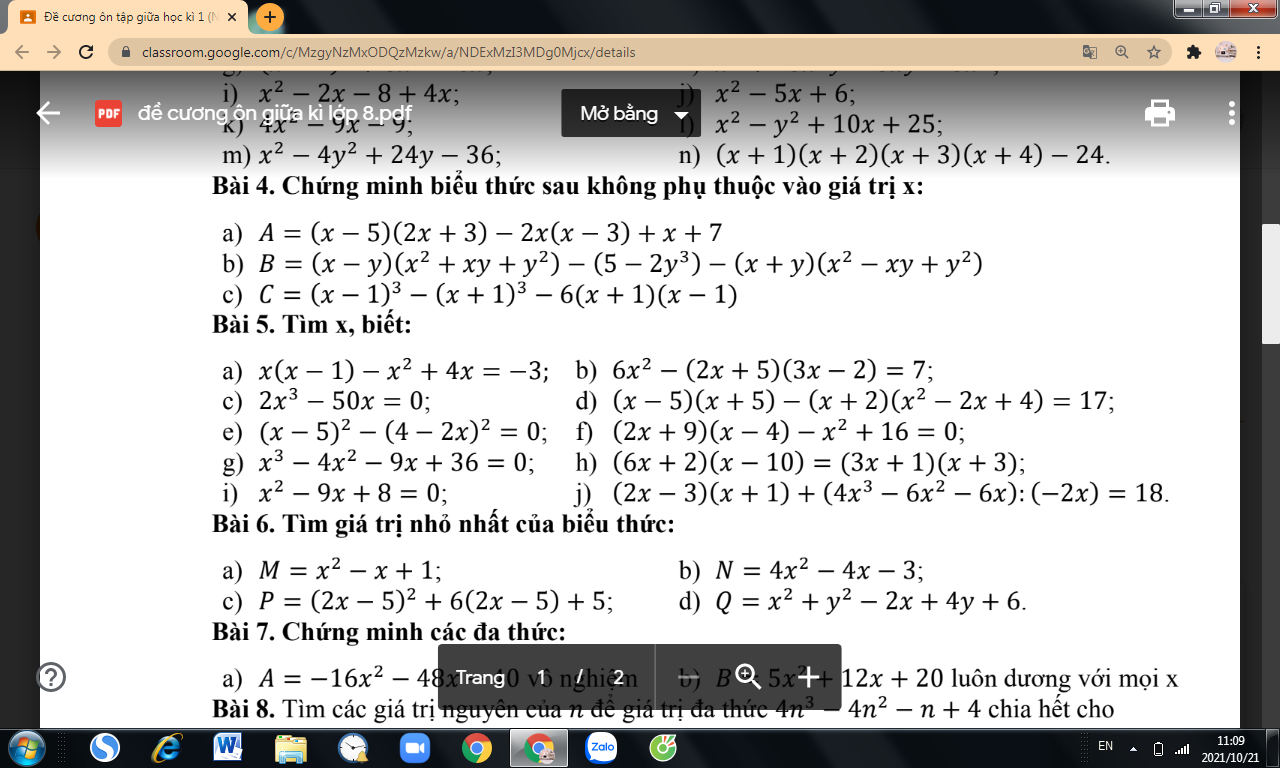
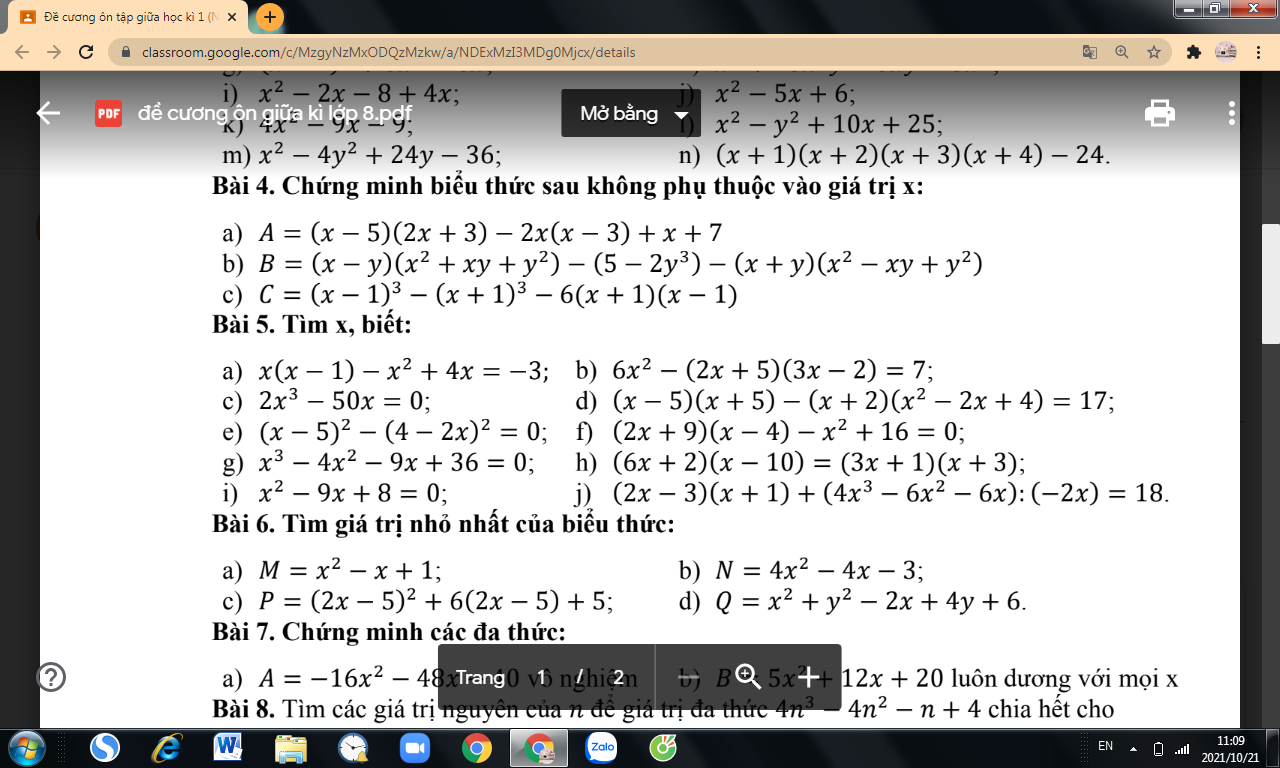
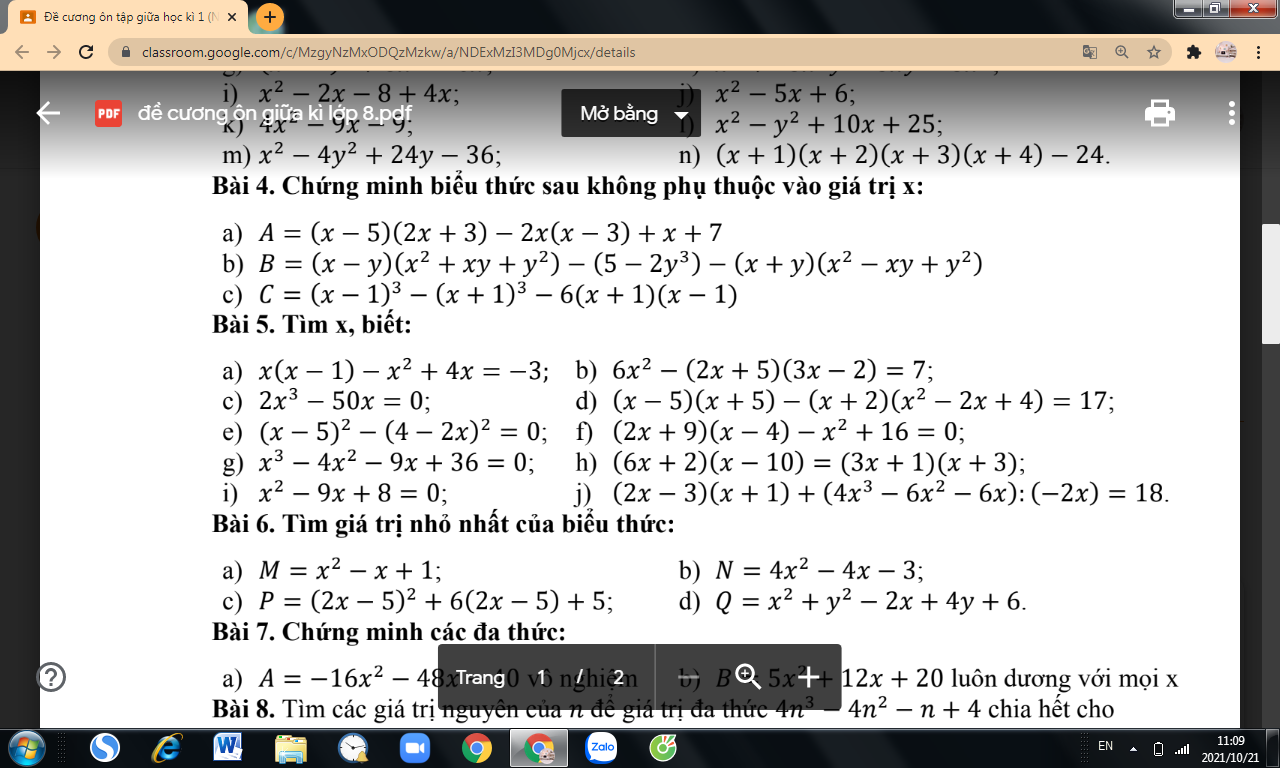
a) \(x\left(x-1\right)-x^2+4x=-3\\ \Rightarrow3x=-3\\ \Rightarrow x=-1\)
b) \(6x^2-\left(2x+5\right)\left(3x-2\right)=7\\ \Rightarrow6x^2-\left(6x^2+15x-4x-10\right)=7\\ \Rightarrow-11x+10=7\\ \Rightarrow x=\dfrac{3}{11}\)
c) \(2x^3-50x=0\\ \Rightarrow2x\left(x^2-50\right)=0\\ \Rightarrow\left[{}\begin{matrix}2x=0\\x^2-50=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=-5\sqrt{2}\\x=5\sqrt{2}\end{matrix}\right.\)
e) \(\left(x-5\right)^2-\left(4-2x\right)^2=0\\ \Rightarrow\left(x-5\right)^2=\left(4-2x\right)^2\\ \Rightarrow\left[{}\begin{matrix}x-5=4-2x\\x-5=2x-4\end{matrix}\right.\\ \Leftarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)
f) \(\left(2x+9\right)\left(x-4\right)-x^2+16=0\\ \Rightarrow2x^2+9x-8x-36-x^2+16=0\\ \Rightarrow x^2+x-20=0\\ \Rightarrow\left(x-4\right)\left(x+5\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=4\\x=-5\end{matrix}\right.\)
VT
1
22 tháng 10 2021
Bài 6:
a: \(M=x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
VT
1
22 tháng 10 2021
a: \(x\left(x-1\right)-x^2+4x=-3\)
\(\Leftrightarrow x^2-x-x^2+4x=-3\)
hay x=-1
5. \(10x^2+24xy-28x+16y^2-24y+41\)
\(=x^2-10x+25+9x^2+16y^2+9+24xy-18x-24y+7\)
\(=\left(x-5\right)^2+\left(3x+4y-3\right)^2+7\ge7\)
Dấu \(=\)khi \(\hept{\begin{cases}x-5=0\\3x+4y-3=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=5\\y=-3\end{cases}}\)