
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 5:
a) Ta có: A+P=Q
nên A=Q-P
\(=2x^2+5xy-3y^2-6x^2+7xy-4y^2\)
\(=-4x^2+12xy-7y^2\)
b) Ta có: B-Q=P
nên B=P+Q
\(=6x^2-7xy+4y^2+2x^2+5xy-3y^2\)
\(=8x^2-2xy+y^2\)
Bài 6:
a) \(P\left(-\dfrac{1}{2}\right)=4\cdot\left(-\dfrac{1}{2}\right)^2-9\cdot\dfrac{-1}{2}=4\cdot\dfrac{1}{4}+\dfrac{9}{2}=1+\dfrac{9}{2}=\dfrac{11}{2}\)
\(Q\left(\dfrac{2}{3}\right)=3\cdot\dfrac{2}{3}+6=2+6=8\)
b) Đặt P(x)=0
\(\Leftrightarrow x\left(4x-9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{9}{4}\end{matrix}\right.\)
Đặt Q(x)=0
\(\Leftrightarrow3x+6=0\)
hay x=-2
B5:
a)ta có :A+P=Q suy ra A=Q-P
A=-4x^2+12xy-y^2
b)ta có :B-Q=P suy ra A=Q+P
B=8x^2-2xy+y^2


TH1 x am
x+(-x)=1.5
x-x=1.5
x=3
TH2 x duong
x+x=1.5
2x=1.5
x=0.75
Vay x=3 hoac x=0.75

\(\frac{1}{2.7}+\frac{1}{7.12}+\frac{1}{12.17}+....+\frac{1}{2012.2017}\)
\(=\frac{1}{5}\left(\frac{5}{2.7}+\frac{5}{7.12}+\frac{5}{12.17}+....+\frac{5}{2012.2017}\right)\)
\(=\frac{1}{5}\left(\frac{1}{2}-\frac{1}{7}+\frac{1}{7}-\frac{1}{12}+....+\frac{1}{2012}-\frac{1}{2017}\right)\)
\(=\frac{1}{5}\left(\frac{1}{2}-\frac{1}{2017}\right)\)
\(=\frac{1}{5}.\frac{2015}{4034}=\frac{403}{4034}\)
ĐẶT A=DÃY SỐ TRÊN=>5A=5/2.7+........+5/2012.2017
=>A=1/2-1/7........-1/2012-1/2017 RÚT GỌN TA ĐƯỢC A=1/2-1/2017


\(\frac{1}{4}\) và \(\frac{1}{2}\)
Vì 0x = 0 (Với mọi \(x\in R\)); 12x = 1 (Với mọi \(x\in Z\)).

a) Ta có: A1=B1
mà 2 góc này ở vị trí đồng vị
⇒ AB//CD
b) AB//CD, AD⊥CD ⇒AD⊥AB
c) Vì AB//CD
⇒ B2+C3=1800(trong cùng phía)
Mà \(C_3=\dfrac{7}{11}B_2\)
\(\Rightarrow B_2=\dfrac{180^0.11}{18}=110^0\)
\(\Rightarrow C_3=180^0-110^0=70^0\)

\(A=2\left(x+1\right)^2+1>=1\forall x\)
Dấu '=' xảy ra khi x=-1
\(B=-3\left(x+1\right)^2-1< =-1\forall x\)
Dấu '=' xảy ra khi x=-1
\(C=\left(2x-3\right)^2+\left(y-\dfrac{1}{2}\right)^2+2020>=2020\forall x,y\)
Dấu '=' xảy ra khi x=3/2 và y=1/2
\(2\left(x+1\right)^2+1>=1\forall x\)
=>E<=1
Dấu '=' xảy ra khi x=-1


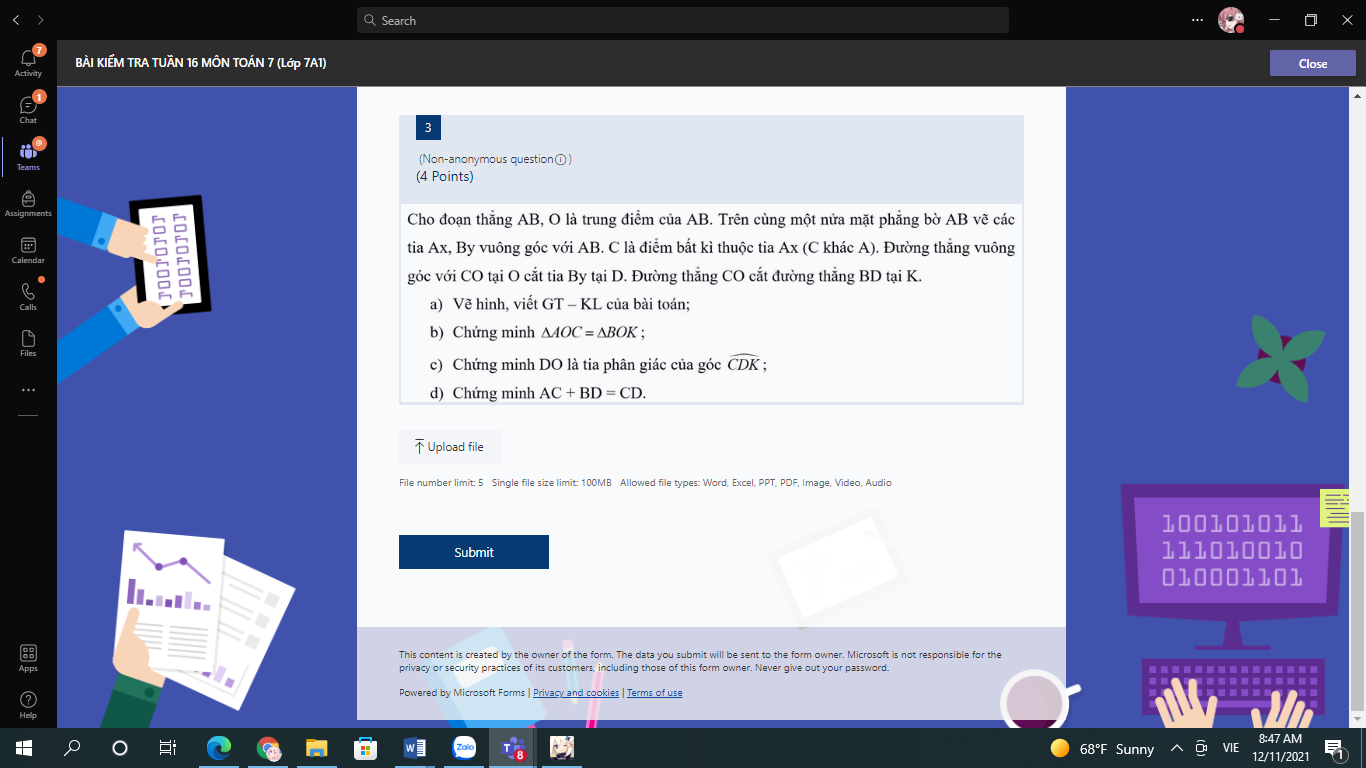
 giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
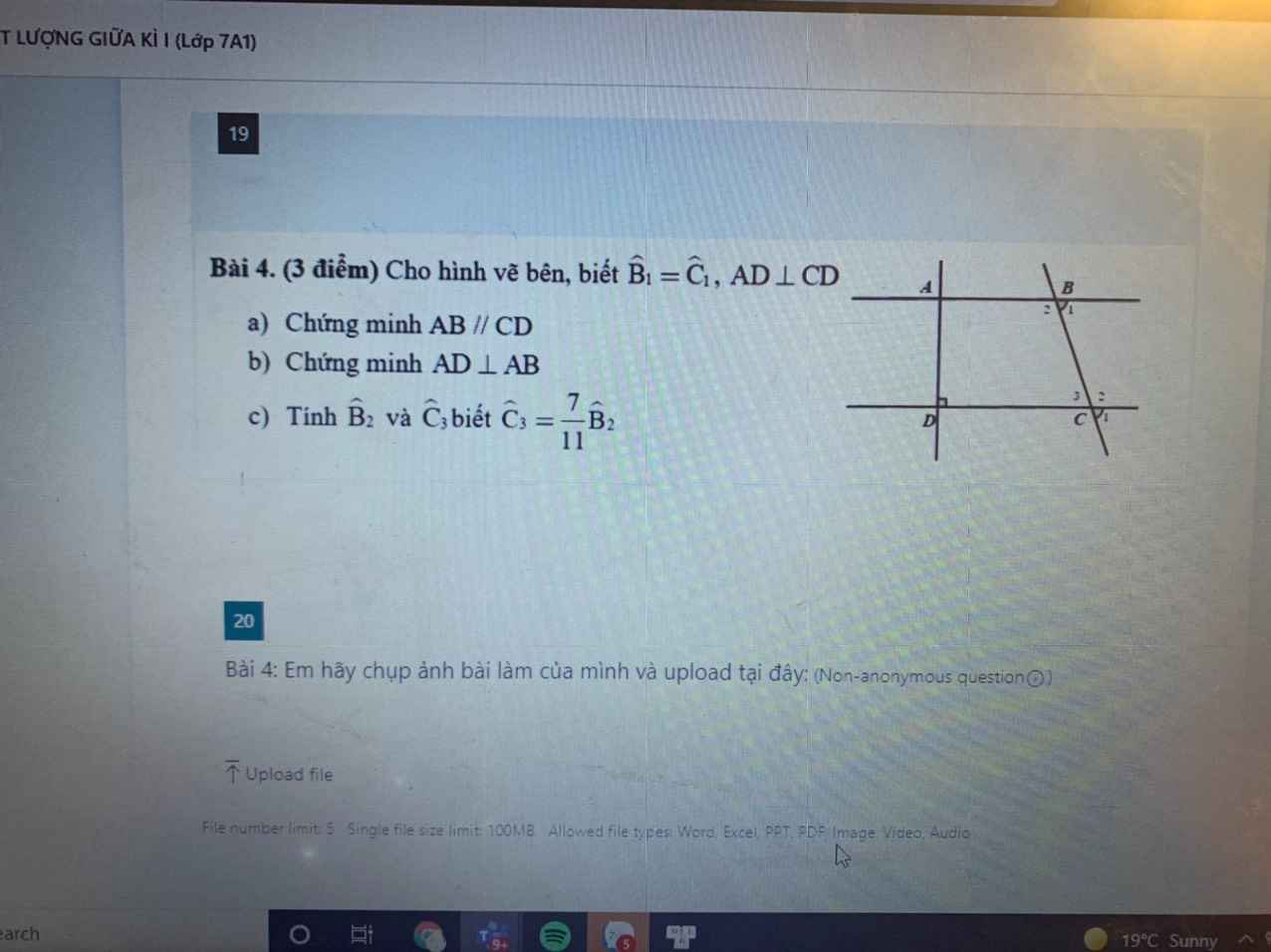

chụp xấu thế ai nhìn đc