
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 1: `m = 3 + 3^2 + ... + 3^2019`.
`= 3(1+3+3^2) + 3^4(1+3+3^2) + 3^7(1+3+3^2) + ... + 3^2017(1+3+3^2)`
`= 13 . 3 + 13 . 3^4 + 3^7 . 13 + ... + 3^2017 .13`
`= 13(3+3^4+3^7+...+3^2017) vdots 13`.
Bài 4: `(n+2021^2022)(n+2022^2021)`
`@ n cancel vdots 2 => n + 2021^2022 equiv 1 + 1 equiv 2 equiv 0 ( mod 2)`
`@ n vdots 2 <=> n + 2022^2021 equiv 0 + 0 equiv 0 ( mod 2)`
Vậy ta có dpcm

Lời giải:
4.
$29(19-13)-19(29-13)=29.19-29.13-(19.29-19.13)$
$=29.19-29.13-19.29+19.13=(29.19-19.29)-(29.13-19.13)$
$=0-13(29-19)=0-13.10=-130$
5.
$31(-18)+31(-81)-31=31[(-18)+(-81)-1]=31[-(18+81)-1]=31(-100)=-3100$
6.
$(-12).47+(-12).52+(-12)=(-12)(47+52+1)=(-12).100=-1200$
7.
$13(23+22)-3(17+28)=13.45-3.45=45(13-3)=45.10=450$

Vì x-7 là ước của x-9 \(\Rightarrow\hept{\begin{cases}x-9⋮x-7\\x-7⋮x-7\end{cases}}\)
\(\Rightarrow x-9-x+7⋮x-7\)
\(\Leftrightarrow-2⋮x-7\)
\(\Rightarrow x-7\in\left\{\pm1;\pm2\right\}\)
\(\Leftrightarrow x\in\left\{-8;-6;-5;-9\right\}\)

c) C=(151515/161616 + 17^9/17^10)-(1500/1600 - 1616/1717)
=(15/16 + 1/17)-(15/16 - 16/17)
= 15/16 ( 1/17 + 16/17)
=15/16 . 1 = 15/16

a: \(\Leftrightarrow n+2\in\left\{1;-1;5;-5\right\}\)
hay \(n\in\left\{-1;-3;3;-7\right\}\)
b: \(\Leftrightarrow n-1-2⋮n-1\)
\(\Leftrightarrow n-1\in\left\{1;-1;2;-2\right\}\)
hay \(n\in\left\{2;0;3;-1\right\}\)
c: \(\Leftrightarrow3n-6+8⋮n-2\)
\(\Leftrightarrow n-2\in\left\{1;-1;2;-2;4;-4;8;-8\right\}\)
hay \(n\in\left\{3;1;4;0;6;-2;10;-6\right\}\)

1: Để C là số nguyên thì 2n+2-3 chia hết cho n+1
=>\(n+1\in\left\{1;-1;3;-3\right\}\)
=>\(n\in\left\{0;-2;2;-4\right\}\)

 Ai làm được mik tích cho, hạn là ngày hôm nay (Cứu!!!!!!)
Ai làm được mik tích cho, hạn là ngày hôm nay (Cứu!!!!!!)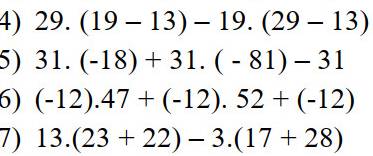
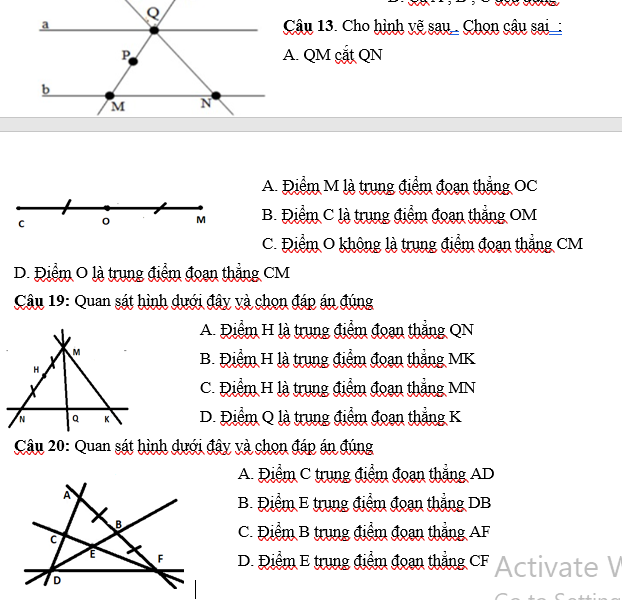 cứu mik với ạ
cứu mik với ạ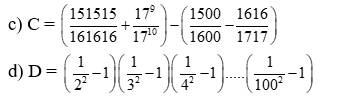

bài tập về nhà thì bạn tự làm