Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Nối \(A,M.\) Vì \(AH\perp BC,MD\perp AC\to A,H,M,D\) cùng nằm trên đường tròn đường kính \(AM\). Suy ra \(\angle MDH=\angle MAH\) (hai góc nội tiếp cùng chắn một cung). Do \(B,M\) đối xứng nhau qua điểm \(H\) nên
\(\angle MAH=\angle BAH\to\angle MAH=\angle ACB\to\angle MDH=\angle ACB.\)
Do \(O\) là trung điểm \(MC\), nên áp dụng tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông \(MCD\), ta được \(\Delta OCD\) cân, suy ra \(\angle ODC=\angle OCD\to\angle ODC=\angle MDH.\) Mà \(\angle ODC+\angle ODM=90^{\circ}\to\angle ODH=90^{\circ}.\) Vậy tam giác \(HDO\) vuông ở \(D.\)
b) Kẻ đường cao \(DK\) của tam giác \(HDO,K\in BC.\) Ta có \(OH=OM+HM=\frac{1}{2}BM+\frac{1}{2}CM=\frac{1}{2}BC.\) Do đó diện tích tam giác \(HDO\) lớn nhất khi và chỉ khi \(DK\) lớn nhất. Gọi \(J\) là trung điểm của \(OH\to DK\le DJ=\frac{1}{2}OH=\frac{1}{4}BC.\) Vậy \(DK\) lớn nhất khi \(K\equiv J\Leftrightarrow\Delta HDO\) vuông cân ở \(D.\) Khi đó \(\angle MAC=45^{\circ}\) (Vì bằng \(\angle DHC,\) góc nội tiếp cùng chắn 1 cung). Suy ra
\(\angle BAM=45^{\circ}\to\angle ABC=67,5^{\circ}\to\angle ACB=22,5^{\circ}.\)
Lấy \(I\) là trung điểm \(BC\to AI=\frac{1}{2}BC=a,\angle AIB=2\angle ACB=45^{\circ}.\) Suy ra \(AH=AI\cdot\sin\angle AIB=a\cdot\sin45^{\circ}=\frac{a\sqrt{2}}{2}.\)
Vậy để diện tích \(HDO\) lớn nhất thì \(AH=\frac{a\sqrt{2}}{2}.\)

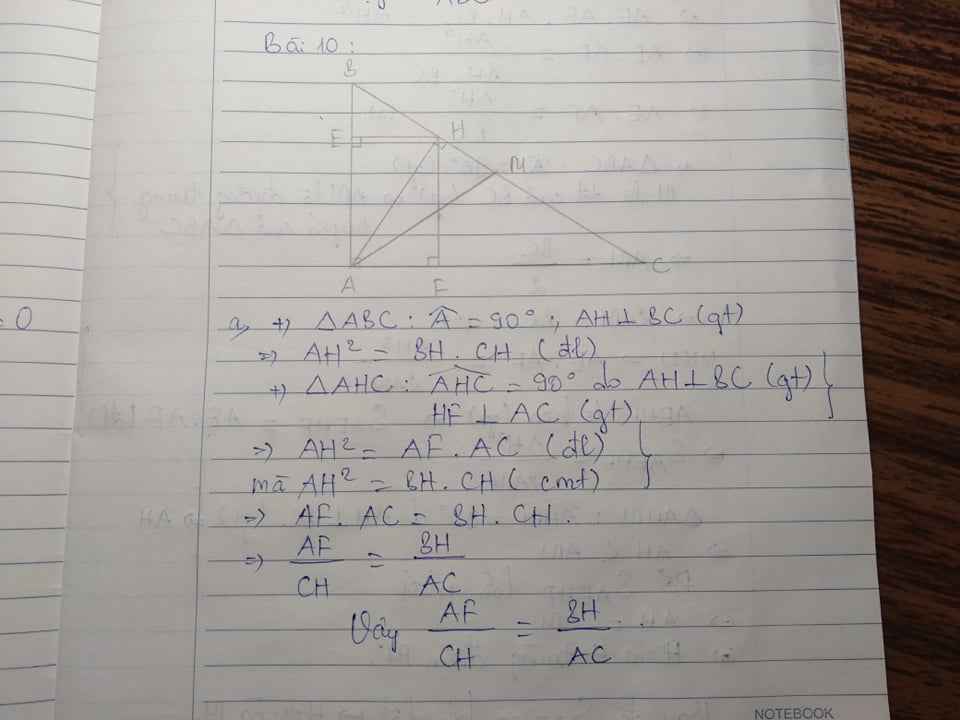
a) Xét ΔAHB vuông tại H có HE là đường cao ứng với cạnh AB(gt)
nên \(AH^2=AE\cdot AB\)(định lí 1 về hệ thức lượng trong tam giác vuông)(1)
Xét ΔAHC vuông tại H có HF là đường cao ứng với cạnh AC(gt)
nên \(AF\cdot AC=AH^2\)(định lí 1 về hệ thức lượng trong tam giác vuông)(2)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)(đpcm)
b) Ta có: \(AE\cdot AB=AF\cdot AC\)(cmt)
\(\Rightarrow\frac{AE}{AC}=\frac{AF}{AB}\)
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
\(\frac{AE}{AC}=\frac{AF}{AB}\)(cmt)
Do đó: ΔAEF∼ΔACB(c-g-c)
⇒\(\widehat{AEF}=\widehat{ACB}\)(3)
Xét ΔABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC(gt)
nên \(AM=\frac{BC}{2}\)(định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(CM=\frac{BC}{2}\)(M là trung điểm của BC)
nên AM=CM
Xét ΔAMC có AM=CM(cmt)
nên ΔAMC cân tại M(định nghĩa tam giác cân)
⇒\(\widehat{C}=\widehat{MAC}\)(hai góc ở đáy)(4)
Từ (3) và (4) suy ra \(\widehat{AEF}=\widehat{MAC}\)
Xét ΔAFE vuông tại A có \(\widehat{AFE}+\widehat{AEF}=90^0\)(hai góc nhọn phụ nhau)
mà \(\widehat{AEF}=\widehat{MAC}\)(cmt)
nên \(\widehat{AFE}+\widehat{MAC}=90^0\)
hay \(\widehat{AFI}+\widehat{IAF}=90^0\)
Xét ΔAIF có \(\widehat{AFI}+\widehat{IAF}=90^0\)(cmt)
nên ΔAIF vuông tại I(định lí đảo của tam giác vuông)
⇒IA⊥IF
hay AM⊥EF(đpcm)