K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 11 2021
Đặt \(A=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+\dfrac{1}{2^4}+\dfrac{1}{2^5}+\dfrac{1}{2^6}\)
\(\Rightarrow2A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+\dfrac{1}{2^4}+\dfrac{1}{2^5}\)
\(\Rightarrow A=2A-A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^5}-\dfrac{1}{2}-\dfrac{1}{2^2}-...-\dfrac{1}{2^6}=1-\dfrac{1}{2^6}\)
CM
24 tháng 6 2017
Cộng thêm 1/2 vào biểu thức đã cho, có:
S + 1/2= 1/2+1/4+ 1/8+ 1/16+1/32+1/64+1/128
Nhận xét:
NM
4
8 tháng 11 2017
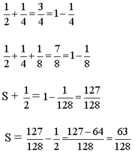
Ta có:2A=\(2+1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}\)
2A-A=\(\left(2+1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}\right)-\left(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\right)\)
\(=2-\frac{1}{32}=\frac{63}{32}=A\)
LJ
8 tháng 11 2017
Ta có: \(A=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\)
\(\Rightarrow A=1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+\frac{1}{2^5}\)
\(\Rightarrow2A=2+1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}\)
\(\Rightarrow2A-A=\left(2+1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}\right)-\left(1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}+\frac{1}{2^5}\right)\)
\(\Rightarrow A=1-\frac{1}{2^5}=\frac{31}{32}\)
Vậy \(A=\frac{31}{32}\)
NT
0
12 tháng 9 2018
Ta có : A = 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64
=> 2A = 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32
=> 2A - A = 1 - 1/64
=> A = 1 - 1/64
=> A = 63/64
1 tháng 3 2017
Đặt \(A=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\)
\(\Rightarrow2A=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\)
\(\Rightarrow2A-A=1-\frac{1}{128}=\frac{127}{128}\)
DN
1
HT
15 tháng 7 2015
Bạn kiểm tra lại đề hộ. Nếu có phân số \(\frac{1}{4}\)thì chịu còn không có thì dễ.
AN
2
nhân A lên 2A sau đó lấy 2A-A là đc :
2A =1+1/2+.....+1/32
2A-A=(1+1/2+.....+1/32)-(1/2+1/4+.....+1/32+1/64)
A=1-1/64
A=63/64
\(A=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\)
\(2A=\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\right)\times2\)
\(2A=\frac{1}{2}\times2+\frac{1}{4}\times2+\frac{1}{8}\times2+\frac{1}{16}\times2+\frac{1}{32}\times2+\frac{1}{64}\times2\)
\(2A=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\)
\(2A-A=\left(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\right)-\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\right)\)
\(A=1-\frac{1}{64}\)
\(A=\frac{63}{64}\)