Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2: Tọa độ điểm A là:
\(\left\{{}\begin{matrix}y_A=0\\-x_A+1=0\end{matrix}\right.\Leftrightarrow A\left(1;0\right)\)
Tọa độ điểm B là:
\(\left\{{}\begin{matrix}x_B=0\\y_B=-0+1=1\end{matrix}\right.\)
Vậy: B(0;1)
\(S_{OAB}=\dfrac{OA\cdot OB}{2}=\dfrac{1}{2}\)
3: Vì (d')//(d) nên a=-1
Vậy: (d'): y=-x+b
Thay x=0 và y=-2 vào (d'), ta được:
b-0=-2
hay b=-2

3: Vì (d')//(d) nên a=-1
Vậy: (d'): y=-x+b
Thay x=0 và y=-2 vào (d'), ta được:
b-0=-2
hay b=-2
Lời giải:
1. Đồ thị $y=-x+1$ có dạng như sau:
2. $A\in Ox$ nên $y_A=0$
Ta có: $y_A=-x_A+1\Leftrightarrow 0=-x_A+1\Leftrightarrow x_A=1$
$B\in Oy$ nên $x_B=0$
Ta có: $y_B=-x_B+1=-0+1=1$
Diện tích tam giác $OAB$:
$S=\frac{1}{2}OA.OB=\frac{1}{2}|x_A|.|y_B|=\frac{1}{2}.1.1=\frac{1}{2}$ (đơn vị diện tích)
3.
Vì $(d')$ song song với $(d)$ nên nó có dạng $y=-x+m$
Tung độ gốc $=-2$ tức là $m=-2$
Vậy $(d'): y=-x-2$

b: Tọa độ M là:
x=0 và y=1-3/2*0=1
Vì (d) đi qua M(0;1) và N(2;3) nên ta có hệ:
0a+b=1 và 2a+b=3
=>b=1; a=1

a: 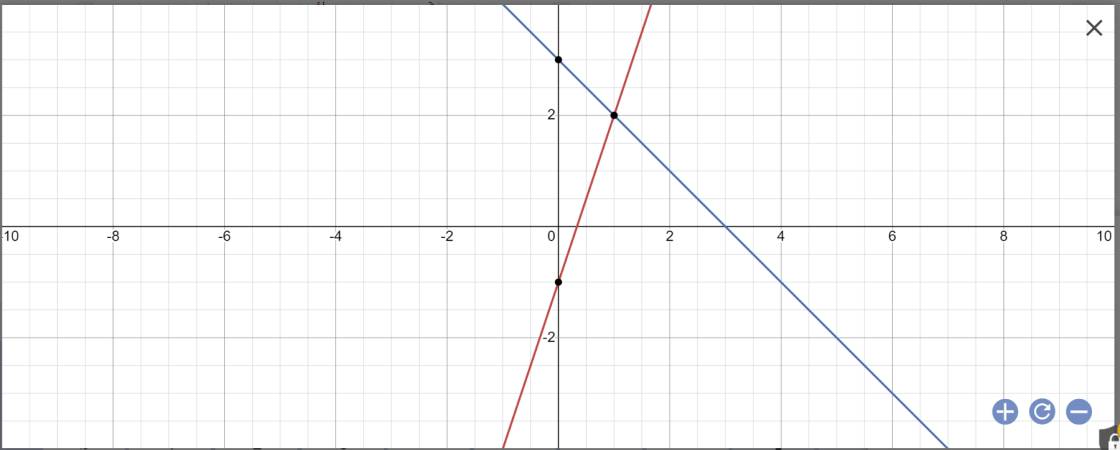
b: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\3x-1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=0\end{matrix}\right.\)
Vậy: A(1/3;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\-x+3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\-x=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=3\end{matrix}\right.\)
Vậy: B(3;0)
Tọa độ C là:
\(\left\{{}\begin{matrix}3x-1=-x+3\\y=3x-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x=4\\y=3x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\cdot1-1=2\end{matrix}\right.\)
Vậy: C(1;2)
c: Gọi \(\alpha\) là góc tạo bởi (d1) với trục Ox
\(tan\alpha=a=3\)
=>\(\alpha\simeq71^033'\)