Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/
l2x+3l=x+2(1)
ta co l2x+3l=\(\hept{\begin{cases}2x+3voix\ge\frac{-3}{2}\\-2x-3voix< \frac{-3}{2}\end{cases}}\)
TH1: neu x>= -3/2 thi (1) <=>2x+3=x+2=>x=-1(chon)
TH2: neu x<= -3/2 thi (1) <=> -2x-3=x+2=>-3x=5=>x=-5/3(chon)
2/
de A dat gtnn thi lx-2006l va l2007l dat gtnn
ma lx-2006l va l2007-xl >=0
=> gtnn cua lx-2006l=0;l2007-xl=0
=> x=2006 hoac 2007
=> gtnn A=1

a) \(\left|2x+3\right|=x+2\)
\(TH1:2x+3=x+2\)
\(\Rightarrow2x-x=2-3\)
\(x=-1\)
\(TH2:2x+3=-\left(x+2\right)\)
\(2x+3=-x-2\)
\(2x+x=-2-3\)
\(3x=-5\)
\(x=\frac{-5}{3}\)
KL: x= -1; x= -5/3
b) bn tham khảo câu này nha
gõ link : http://olm.vn/hoi-dap/question/650540.html
CHÚC BN HỌC TỐT!!!



\(A=\left|x-2006\right|+\left|2007-x\right|\ge\left|x-2006+2007-x\right|=\left|1\right|=1\)
\(minA=1\Leftrightarrow\left(x-2006\right)\left(2007-x\right)\ge0\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-2006\ge0\\2007-x\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-2006\le0\\2007-x\le0\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow2006\le x\le2007\)

\(A=\left|x-2006\right|+\left|2007-x\right|\)
Vì \(x>2007\) nên \(2x-4013>4014-4013=1\)
\(\Rightarrow A>1\)
Vậy \(A_{min}=1\Leftrightarrow2006\le x\le2007\)

Áp dụng bđt \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\)
\(A\ge\left|x-2016+2017-x\right|=1\)
Vậy minA=1
Ta có \(A=\left|x-2006\right|+\left|2007-x\right|\)
\(=\left|2006-x\right|+\left|x-2007\right|\)
Ta có \(A=\left|2006-x\right|+\left|x-2007\right|\ge\left|2006-x+x-2007\right|=1\)
Dấu "=" xảy ra khi và chỉ \(2006\le x\le2007\)
Vậy GTNN A=1 khi \(2006\le x\le2007\)

Ta có :
\(A=\left|x-2006\right|+\left|2007-x\right|\ge\left|x-2006+2007-x\right|\)
\(\Rightarrow A\ge1\)
\(\Rightarrow A_{min}=1\)
\(\Leftrightarrow\left(x-2006\right)\left(2007-x\right)\ge0\)
Ta có bảng xét dấu :
\(\Rightarrow2006\le x\le2007\)
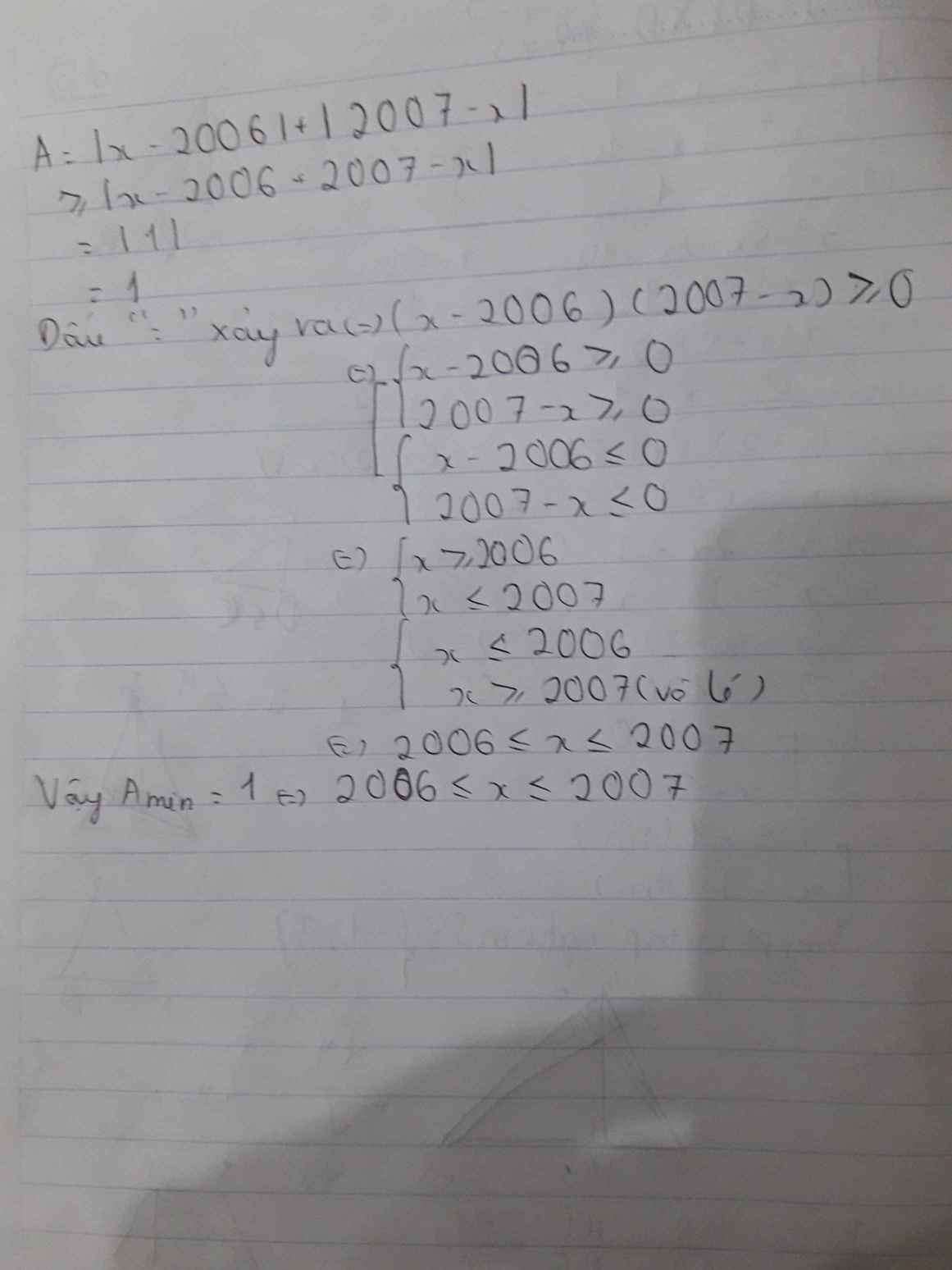
Bài giải
'THAM KHẢO
a,
Điều kiện: x+2≥0⇔x≥−2x+2≥0⇔x≥-2
|2x+3|=x+2|2x+3|=x+2
⇔[2x+3=x+22x+3=−x−2⇔[2x+3=x+22x+3=−x−2
⇔[x=−13x=−5⇔[x=−13x=−5
⇔⎡⎣x=−1(t/m)x=−53(t/m)⇔[x=−1(t/m)x=−53(t/m)
Vậy x∈{−1;−53}x∈{-1;-53}
b,
A=|x−2006|+|2007−x|≥|x−2006+2007−x|=|1|=1A=|x−2006|+|2007−x|≥|x−2006+2007−x|=|1|=1
Đẳng thức xảy ra ⇔(x−2006)(2007−x)≥0⇔(x−2006)(2007−x)≥0
⇔(x−2006)(x−2007)≤0⇔(x−2006)(x−2007)≤0
Vì x−2006>x−2007x−2006>x−2007
⇒{x−2006≥0x−2007≤0⇒{x−2006≥0x−2007≤0
⇔{x≥2006x≤2007⇔{x≥2006x≤2007
⇔2006≤x≤2007⇔2006≤x≤2007
Vậy Amin=1⇔2006≤x≤2007