Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

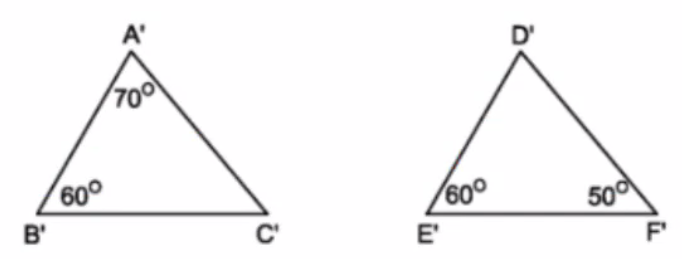
Xét \(\Delta D'E'F':\)
\(\widehat{D'}+\widehat{E'}+\widehat{F'}=180^o\) (Tổng 3 góc trong tam giác).
\(\Rightarrow\widehat{D'}+60^o+50^o=180^o.\\ \Rightarrow\widehat{D'}=70^o.\\ \Rightarrow\widehat{D'}=\widehat{A'}\left(=70^o\right).\)
Xét \(\Delta A'B'C'\) và \(\Delta D'E'F':\)
\(\widehat{A'}=\widehat{D'}\left(cmt\right).\)
\(\widehat{B'}=\widehat{E'}\left(=60^o\right).\)
\(\Rightarrow\) \(\Delta A'B'C'\sim\) \(\Delta D'E'F'\left(g-g\right).\)
\(\Rightarrow\dfrac{B'C'}{E'F'}=\dfrac{A'C'}{D'F'}\) (2 cạnh tương ứng).
\(\Rightarrow B'C'.D'F'=A'C'.E'F'.\)

a: Xét tứ giác AB'CM có
E là trung điểm chung của AC và B'M
nên AB'CM là hình bình hành
Suy ra: AB'//MC và AB'=MC
Xét tứ giác BMCA' có
D là trung điểm của MA' và BC
nên BMCA' là hình bình hành
Suy ra: CM//BA' và MC=BA'
=>AB'//BA' và AB'=BA'
=>AB'A'B là hình bình hành
b: Xét tứ giác AMBC' có
F là trung điểm chung của AB và MC'
nên AMBC' là hình bình hành
SUy ra: AM//BC' và AM=BC'
=>BC'//B'C và BC'=B'C
=>BC'B'C là hình bình hành
Suy ra: BB' và CC' cắt nhau tại trung điểm của mỗi đường
=>C' và C đối xứng nhau qua O

a: Xét tứ gíc AB'CM có
E là trung điểm chung của AC và B'M
nên AB'CM là hình bình hành
Suy ra: AB'//CM và AB'=CM
Xét tứ giác BMCA' có
D là trung điểm chung của BC và MA'
nên BMCA' là hình bình hành
Suy ra: BA'//CM và BA'=CM
=>AB'//BA' và AB'=BA'
=>AB'A'B' là hình bình hành
b: Xét tứ giác AMBC' có
F là trung điểm chung của AB và MC'
nên AMBC' là hình bình hành
Suy ra: AM//CB'//B'C và BC'=B'C
=>BC'B'C là hình bình hành
Suy ra: BB' và CC' cắt nhau tại trung điểm của mỗi đường
=>O là trung điểm của CC'

a) Vì \(\Delta ABC \backsim \Delta A'B'C'\) theo tỉ số đồng dạng \(k\) nên \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = k;\,\,\widehat B = \widehat {B'}\)
Mà AM và A’M’ lần lượt là trung tuyến của hai tam giác ABC và A’B’C’ nên M và M’ lần lượt là trung điểm của BC và B’C’.
\(\begin{array}{l} \Rightarrow BM = \frac{1}{2}BC;\,\,B'M' = \frac{1}{2}B'C'\\ \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{BM}}{{B'M'}} = k\end{array}\)
Xét tam giác ABM và tam giác A’B’M’ có:
\(\frac{{AB}}{{A'B'}} = \frac{{BM}}{{B'M'}}\) và \(\widehat B = \widehat {B'}\)
\( \Rightarrow \Delta ABM \backsim \Delta A'B'M'\) (c-g-c)
\( \Rightarrow \frac{{AM}}{{A'M'}} = \frac{{BM}}{{B'M'}} = k\)
b) Vì \(\Delta ABC \backsim \Delta A'B'C'\) theo tỉ số đồng dạng \(k\) nên \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = k;\,\,\widehat B = \widehat {B'}\)
\(\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}}\)
Vì AD và A’D’ lần lượt là phân giác của tam giác ABC và tam giác A’B’C’ nên ta có \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\) và \(\frac{{D'B'}}{{D'C'}} = \frac{{A'B'}}{{A'C'}}\)
\( \Rightarrow \frac{{DB}}{{DC}} = \frac{{D'B'}}{{D'C'}} \Rightarrow \frac{{DB}}{{D'B'}} = \frac{{DC}}{{D'C'}} = \frac{{DB + DC}}{{D'B' + D'C'}} = \frac{{BC}}{{B'C'}}\)
Mà \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\) (chứng minh ở câu a) nên \(\frac{{DB}}{{D'B'}} = \frac{{AB}}{{A'B'}}\)
Xét tam giác ABD và tam giác A’B’D’ có:
\(\frac{{BD}}{{B'D'}} = \frac{{AB}}{{A'B'}}\) và \(\widehat B = \widehat {B'}\)
\( \Rightarrow \Delta ABD \backsim \Delta A'B'D'\) (c-g-c)
\( \Rightarrow \frac{{AD}}{{A'D'}} = \frac{{AB}}{{A'B'}} = k\)
c) Ta có \(\widehat B = \widehat {B'}\) và \(\widehat {AHB} = \widehat {A'H'B'} = 90^\circ \)
\( \Rightarrow \Delta ABH \backsim \Delta A'B'H'\) (g-g)
\( \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{AH}}{{A'H'}} = k\)
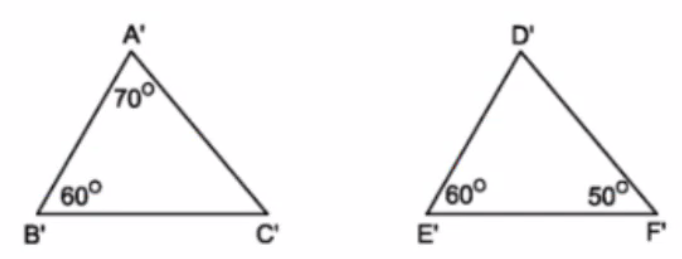
a: \(\widehat{C'}=180^0-60^0-70^0=50^0\)
Xét ΔA'B'C' và ΔD'E'F' có
\(\widehat{B'}=\widehat{E'};\widehat{C'}=\widehat{F'}\)
Do đó:ΔA'B'C'\(\sim\)ΔD'E'F'
b: Ta có: ΔA'B'C'\(\sim\)ΔD'E'F'
nên A'C'/D'F'=B'C'/E'F'
hay \(A'C'\cdot E'F'=B'C'\cdot D'F'\)