Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tọa độ của vectơ \(\overrightarrow u + \overrightarrow v + \overrightarrow w \) là: \(\overrightarrow u + \overrightarrow v + \overrightarrow w = \left( { - 2 + 0 + \left( { - 2} \right);0 + 6 + 3} \right) = \left( { - 4;9} \right)\)
b) Ta có: \(\overrightarrow w + \overrightarrow u = \overrightarrow v \Leftrightarrow \overrightarrow w = \overrightarrow v - \overrightarrow u \) nên \(\overrightarrow w = \left( {0 - \sqrt 3 ; - \sqrt 7 - 0} \right) = \left( { - \sqrt 3 ; - \sqrt 7 } \right)\)

Chọn D.
Ta có: c = 2 a = 1 b 2 = c 2 - a 2 ⇒ a 2 = 1 b 2 = 3
Phương trình (H) : x 2 1 - y 2 3 = 1

Lời giải:
Theo công thức thôi em:
\(A(x_1,y_1); B(x_2,y_2)\Rightarrow \overrightarrow{AB}(x_2-x_1,y_2-y_1)\)
Áp dụng vào bài toán thì \(\overrightarrow {AB}\) có tọa độ $(2,5)$

đặc \(C\left(x_c\overset{.}{,}y_c\right)\)
\(\Rightarrow\overrightarrow{AC}\left(x_c+2\overset{.}{,}y_c\right)\) , \(\overrightarrow{BC}\left(x_c-2\overset{.}{,}y_c\right)\)
vì \(AC\perp BC\Rightarrow\left(x_c+2\right)\left(x_c-2\right)+y_c^2=0\) ..............(1)
ta có : \(\left[{}\begin{matrix}y_G=\dfrac{y_c}{3}=\dfrac{-1}{3}\\y_G=\dfrac{y_c}{3}=\dfrac{1}{3}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}y_c=-1\\y_c=1\end{matrix}\right.\) (vì G là trọng tâm tam giác \(ABC\) và có khoảng cách với \(ox\) là \(\dfrac{1}{3}\)
từ (1) ta có : nếu \(y_c=-1\Rightarrow x_c=\pm\sqrt{3}\) , với \(y_c=1\Rightarrow x_c=\pm\sqrt{3}\)
\(\Rightarrow C\left(-1\overset{.}{,}-\sqrt{3}\right)\) , \(C\left(-1\overset{.}{,}\sqrt{3}\right)\) , \(C\left(1\overset{.}{,}-\sqrt{3}\right)\) , \(C\left(1\overset{.}{,}\sqrt{3}\right)\)
vậy .....................................................................................................................

\(A\subset B\Leftrightarrow\left\{{}\begin{matrix}m\le5\\m+3>7\end{matrix}\right.\) \(\Rightarrow4< m\le5\)
\(B\subset A\Leftrightarrow\left\{{}\begin{matrix}m>5\\m+3\le7\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m>5\\m\le4\end{matrix}\right.\) ko tồn tại m thỏa mãn

\(N\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AN}=\left(x-2;y\right)\\\overrightarrow{BN}=\left(x-1;y-2\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}AN=\sqrt{\left(x-2\right)^2+y^2}=\sqrt{x^2+y^2-4x+4}\\BN=\sqrt{\left(x-1\right)^2+\left(y-2\right)^2}=\sqrt{x^2+y^2-2x-4y+5}\end{matrix}\right.\)
\(AN=2BN\Leftrightarrow AN^2=4BN^2\)
\(\Leftrightarrow x^2+y^2-4x+4=4x^2+4y^2-8x-16y+20\)
\(\Leftrightarrow3x^2+3y^2-4x-16y+16=0\)
\(\Leftrightarrow x^2+y^2-\frac{4}{3}x-\frac{16}{3}y+\frac{16}{3}=0\)
\(\Rightarrow\left\{{}\begin{matrix}a=\frac{2}{3}\\b=\frac{8}{3}\\R^2=a^2+b^2-\frac{16}{3}=\frac{20}{9}\end{matrix}\right.\) \(\Rightarrow a+b+R^2=\frac{50}{9}\)
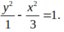
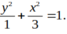
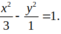
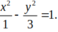
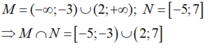
Để tìm giao của hai tập hợp A và B, ta cần xác định phần nằm trong cả hai tập hợp. Ta có:
A = (-2;7]
B = [0;5]
Phần nằm trong cả hai tập hợp là đoạn [-2;5], vì nó nằm trong A và cũng nằm trong B.
Vậy, ta có:
A ∩ B = [-2;5]
CAB là bù của A ∩ B trong tập hợp A hoặc B. Vì vậy, ta có:
CAB = (-∞;-2) U (5;7]
Vậy đáp án là D.CAB=(-2;0)U(5;7].
Để tìm giao của hai tập hợp A và B, ta cần xác định phần nằm trong cả hai tập hợp. Ta có:
A = (-2;7]
B = [0;5]
Phần nằm trong cả hai tập hợp là đoạn [-2;5], vì nó nằm trong A và cũng nằm trong B.
Vậy, ta có:
A ∩ B = [-2;5]
CAB là bù của A ∩ B trong tập hợp A hoặc B. Vì vậy, ta có:
CAB = (-∞;-2) U (5;7]
Vậy đáp án là D.CAB=(-2;0)U(5;7].