Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b)
=>\(\left\{{}\begin{matrix}m-1>2\\m+3\le5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>3\\m\le2\end{matrix}\right.\)(vô lý)
vậy ko tồn tại m

a: \(A\cap B=\left(-3;1\right)\)
\(A\cup B\)=[-5;4]
A\B=[1;4]
\(C_RA\)=R\A=(-∞;-3]\(\cap\)(4;+∞)
b: C={1;-1;5;-5}
\(B\cap C=\left\{-5;-1\right\}\)
Các tập con là ∅; {-5}; {-1}; {-5;-1}


Để A là con của của B thì \(\left\{{}\begin{matrix}m-3>=-3\\m+4< =5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>=0\\m< =1\end{matrix}\right.\)
=>0<=m<=1

\(mx^2-4x+m-3=0\left(1\right)\)
Để tập hợp B có đúng 2 tập con và \(B\subset A\) thì \(\left(1\right)\) có 2 nghiệm phân biệt cùng dương
\(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}\Delta'>0\\P>0\\S>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4-m\left(m-3\right)>0\\\dfrac{m-3}{m}>0\\\dfrac{4}{m}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-3m-4< 0\\m< 0\cup m>3\\m>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1< m< 4\\m< 0\cup m>3\\m>0\end{matrix}\right.\)
\(\Leftrightarrow3< m< 4\)
Ta có:
\(\overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{BG}\)
+) \(\overrightarrow{BG}=\dfrac{1}{3}\left(\overrightarrow{BM}+\overrightarrow{BN}\right)=\dfrac{1}{3}\left(-\dfrac{2}{3}\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CN}\right)\)
\(=\dfrac{1}{3}\left(-\dfrac{2}{3}\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{DC}\right)=\dfrac{1}{3}\left(-\dfrac{13}{6}\overrightarrow{AB}+\overrightarrow{AC}\right)\)
\(=-\dfrac{13}{18}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
=> \(\overrightarrow{AG}=\dfrac{5}{18}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
Mặt khác:
\(\overrightarrow{AI}=\overrightarrow{AB}+\overrightarrow{BI}=\overrightarrow{AB}+k\overrightarrow{BC}=\overrightarrow{AB}+k\left(\overrightarrow{AC}-\overrightarrow{AB}\right)=\left(1-k\right)\overrightarrow{AB}+k\overrightarrow{AC}\)
Để A, G, I thẳng hàng
=>\(\dfrac{\dfrac{5}{18}}{1-k}=\dfrac{\dfrac{1}{3}}{k}\Rightarrow k=\dfrac{6}{11}\)

a) để \(A\subset B\Leftrightarrow\left\{{}\begin{matrix}2m-1\ge-4\\m+3\le5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ge\dfrac{-3}{2}\\m\le2\end{matrix}\right.\Leftrightarrow\dfrac{-3}{2}\le m\le2\)
b) để \(B\subset A\Leftrightarrow\left\{{}\begin{matrix}2m-1\le-4\\m+3\ge5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\le\dfrac{-3}{2}\\m\ge2\end{matrix}\right.\Rightarrow m\in\varnothing\)
c) để \(A\cap B=\varnothing\Leftrightarrow\left[{}\begin{matrix}m+3< 4\\5< 2m-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m< 1\\m>3\end{matrix}\right.\)
\(\Rightarrow m\in\left(-\infty;1\right)\cup\left(3;+\infty\right)\)

Để A hợp B=A thì B là tập con của A
=>2m-5<23 và 23<=-m
=>2m<28 và -m>=23
=>m<=-23 và m<14
=>m<=-23
=>Chọn B
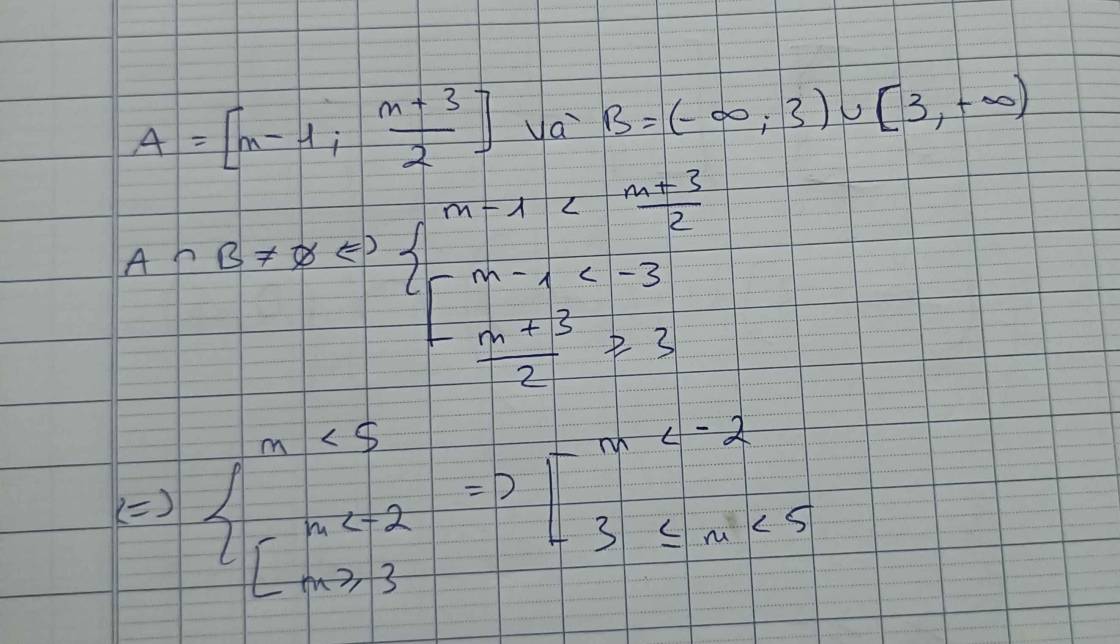

\(A\subset B\Leftrightarrow\left\{{}\begin{matrix}m\le5\\m+3>7\end{matrix}\right.\) \(\Rightarrow4< m\le5\)
\(B\subset A\Leftrightarrow\left\{{}\begin{matrix}m>5\\m+3\le7\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m>5\\m\le4\end{matrix}\right.\) ko tồn tại m thỏa mãn