
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(=\int\limits^1_{-1}\sqrt{\left(e^x-1\right)^2}dx=\int\limits^1_{-1}\left|e^x-1\right|dx=\int\limits^0_{-1}\left(1-e^x\right)dx+\int\limits^1_0\left(e^x-1\right)dx\)
\(=\left(x-e^x\right)|^0_{-1}+\left(e^x-x\right)|^1_0=\dfrac{1}{e}+e-2\)

\(\int_{-1}^1\sqrt{e^{2x}-2e^x+1}dx\)
\(=\int_{-1}^1\left|e^x-1\right|dx\)
\(=\int_{-1}^0\left(1-e^x\right)dx+\int_0^1\left(e^x-1\right)dx\)
\(=\left(x-e^x\right)|^0_{-1}+\left(e^x-x\right)|^1_0\)
\(=\left(\dfrac{1}{e}\right)+\left(e-2\right).\)
\(=\left(\sqrt{e}-\dfrac{1}{\sqrt{e}}\right)^2\)


3. Đồng biến
5. \(n.x^{n-1}\) và \(\dfrac{1}{2\sqrt{x}}\)
6. Dương


Do thiết diện qua trục là hình vuông \(\Rightarrow h=2R\)
Thể tích khối trụ: \(V'=\pi R^2h=2\pi R^3\)
Độ dài cạnh hình vuông nội tiếp trong đường tròn bán kính R: \(a=R\sqrt{2}\)
\(\Rightarrow\)Thể tích khối lăng trụ tứ giác đều:
\(V=a^2.h=2R^2.2R=4R^3\)
\(\Rightarrow\dfrac{V}{V'}=\dfrac{\pi}{2}\)
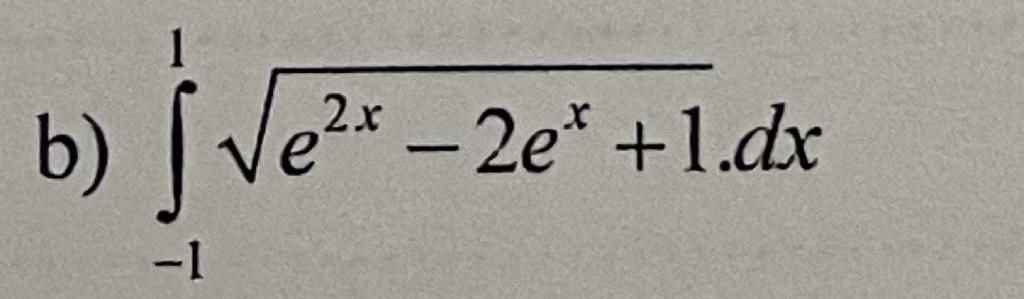 giúp mik với
giúp mik với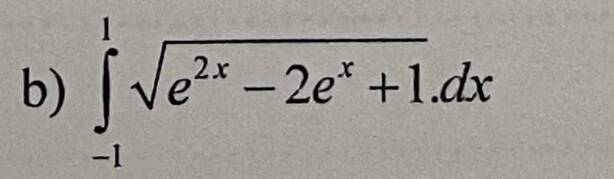




100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000999999999999999999 nha