
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



7a.
\(y'=3x^2-2\left(m-1\right)x-m-3\)
Hàm nghịch biến trên \(\left(-1;0\right)\) khi và chỉ khi \(y'\le0\) ; \(\forall x\in\left(-1;0\right)\)
\(\Leftrightarrow3x^2-2\left(m-1\right)x-m-3\le0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=\left(m-1\right)^2+3\left(m+3\right)>0\\x_1\le-1< 0\le x_2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2+m+10>0\left(\text{luôn đúng}\right)\\f\left(-1\right)\le0\\f\left(0\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3+2\left(m-1\right)-m-3\le0\\-m-3\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m-2\le0\\-m-3\le0\end{matrix}\right.\) \(\Leftrightarrow-3\le m\le2\)
7b.
\(y'=-x^2+2\left(m-1\right)x+m+3\)
Hàm đồng biến trên \(\left(0;3\right)\) khi và chỉ khi \(y'\le0\) ; \(\forall x\in\left(0;3\right)\)
\(\Leftrightarrow-x^2+2\left(m-1\right)x+m+3\ge0\) ; \(\forall x\in\left(0;3\right)\)
\(\Leftrightarrow m\left(2x+1\right)\ge x^2+2x-3\)
\(\Leftrightarrow m\ge\dfrac{x^2+2x-3}{2x+1}\)
\(\Leftrightarrow m\ge\max\limits_{\left[0;3\right]}\dfrac{x^2+2x-3}{2x+1}\)
Xét hàm \(f\left(x\right)=\dfrac{x^2+2x-3}{2x+1}\) trên \(\left(0;3\right)\)
\(f'\left(x\right)=\dfrac{2\left(x^2+x+4\right)}{\left(2x+1\right)^2}>0\) ; \(\forall x\Rightarrow f\left(x\right)\) đồng biến
\(\Rightarrow f\left(x\right)< f\left(3\right)=\dfrac{12}{7}\)
\(\Rightarrow m\ge\dfrac{12}{7}\)

\(\left(1-\dfrac{1}{2}\right)\):\(\left(1-\dfrac{1}{3}\right)\):\(\left(1-\dfrac{1}{4}\right)\):\(\left(1-\dfrac{1}{5}\right)\):\(\left(1-\dfrac{1}{6}\right)\):\(\left(1-\dfrac{1}{7}\right)\)
=\(\left(\dfrac{2-1}{2}\right)\):\(\left(\dfrac{3-1}{3}\right)\):\(\left(\dfrac{4-1}{4}\right)\):\(\left(\dfrac{5-1}{5}\right)\):\(\left(\dfrac{6-1}{6}\right)\)
=\(\dfrac{1}{2}\):\(\dfrac{2}{3}\):\(\dfrac{3}{4}\):\(\dfrac{4}{5}\):\(\dfrac{5}{6}\)
=\(\dfrac{1.\left(3.4.5\right)6}{\left(3.4.5\right)\left(2.2\right)}\)
=\(\dfrac{6}{2.2}=\dfrac{3}{2}\)

xin lỗi nha mình không biết chủ đề nào nên mới chọn đại đây là bài của lớp 7 nha các bạn


\(=\int\limits^1_{-1}\sqrt{\left(e^x-1\right)^2}dx=\int\limits^1_{-1}\left|e^x-1\right|dx=\int\limits^0_{-1}\left(1-e^x\right)dx+\int\limits^1_0\left(e^x-1\right)dx\)
\(=\left(x-e^x\right)|^0_{-1}+\left(e^x-x\right)|^1_0=\dfrac{1}{e}+e-2\)

\(\int_{-1}^1\sqrt{e^{2x}-2e^x+1}dx\)
\(=\int_{-1}^1\left|e^x-1\right|dx\)
\(=\int_{-1}^0\left(1-e^x\right)dx+\int_0^1\left(e^x-1\right)dx\)
\(=\left(x-e^x\right)|^0_{-1}+\left(e^x-x\right)|^1_0\)
\(=\left(\dfrac{1}{e}\right)+\left(e-2\right).\)
\(=\left(\sqrt{e}-\dfrac{1}{\sqrt{e}}\right)^2\)

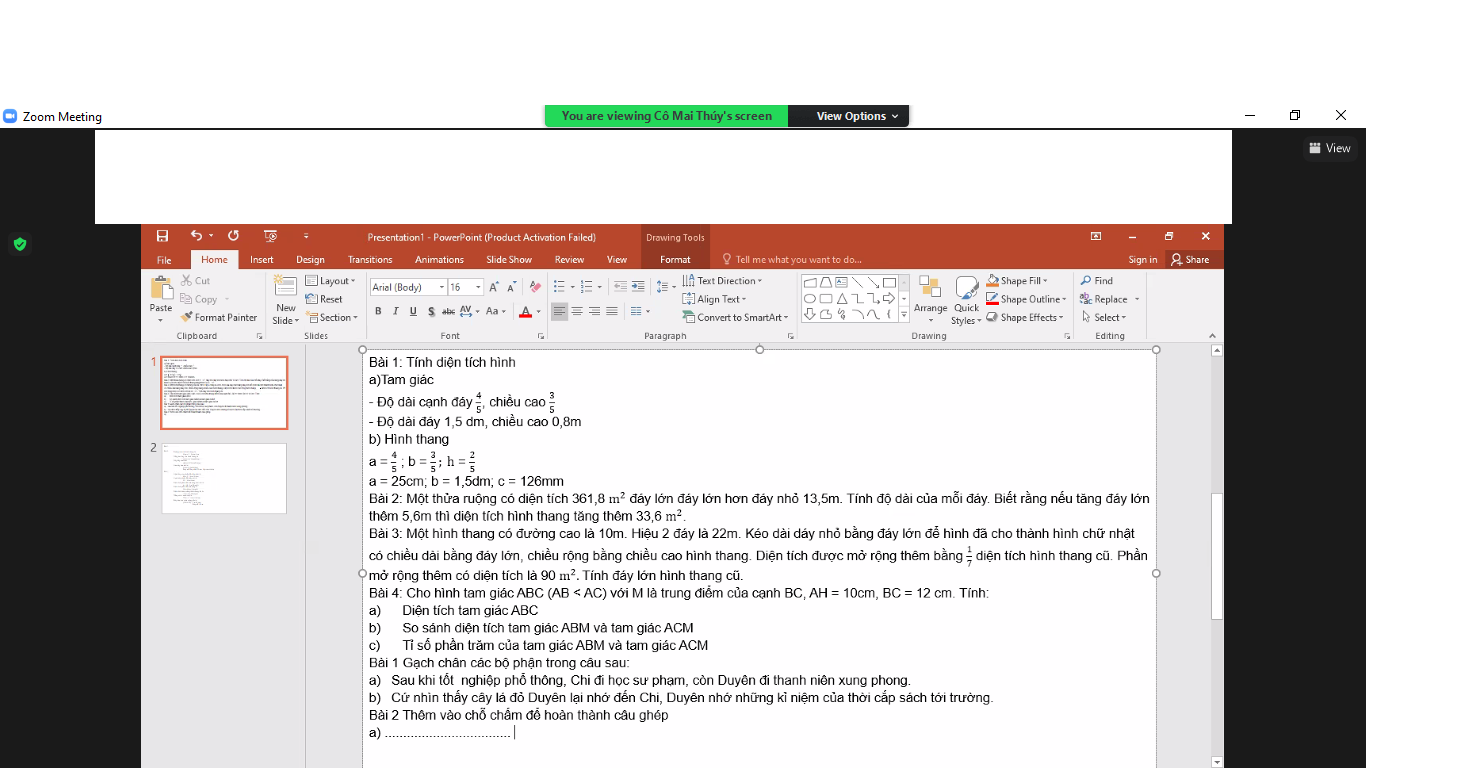


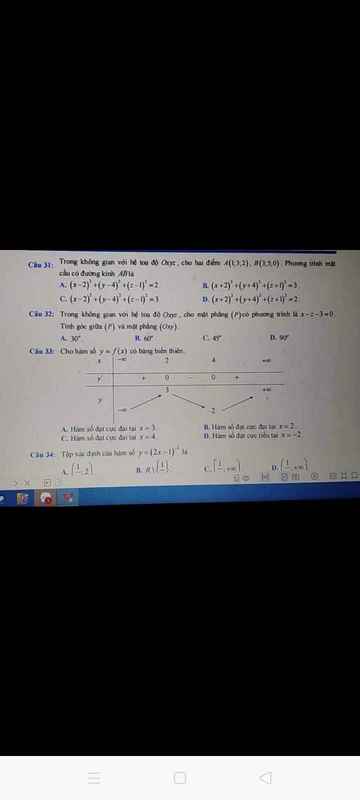
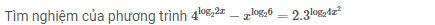
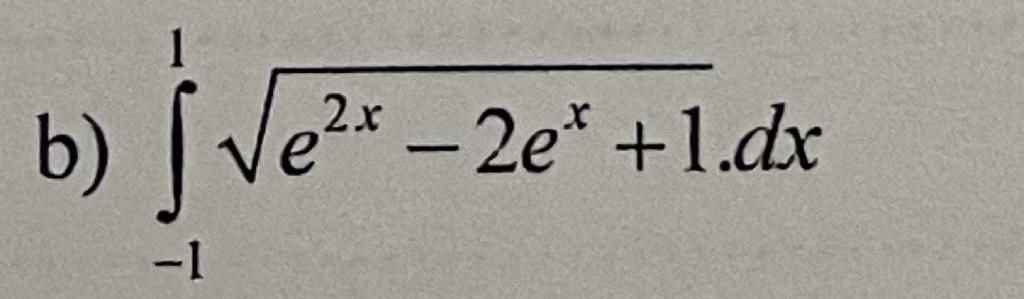 giúp mik với
giúp mik với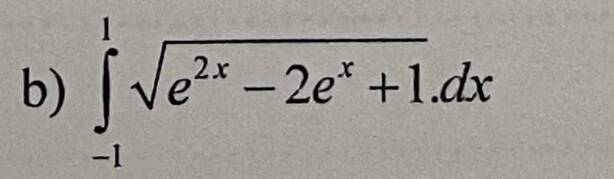

bạn lưu rùi giải giúp mik cái