K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
29 tháng 11 2019
Chọn C
Ta có: ∫ 2 7 f ( x ) d x = ∫ 2 5 f ( x ) d x + ∫ 5 7 f ( x ) d x = 3 + 9 = 12 .
CM
23 tháng 5 2017
Đáp án: A.
§ Hướng dẫn giải:
Gọi N là trung điểm của cạnh đáy AC.
Khi đó BC // (SMN)
⇒ d(SM,BC)=d(B,(SMN))=d(A,(SMN))
Gọi H là hình chiếu vuông góc của A trên đoạn SM.
Ta có thể chứng minh được M N ⊥ ( S A M )
từ đó A H ⊥ ( S M N )
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 1 2022
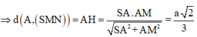
Xét hàm \(f\left(x\right)=\dfrac{1}{9^x-3}+\dfrac{1}{3^x-9}\) có \(f'\left(x\right)=-\dfrac{9^x.ln9}{\left(9^x-3\right)^2}-\dfrac{3^x.ln3}{\left(3^x-9\right)^2}< 0\)
\(\Rightarrow\) Hàm luôn nghịch biến trên miền xác định
\(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=-\dfrac{1}{3}-\dfrac{1}{9}=-\dfrac{4}{9}\) ; \(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=0\) ; \(f\left(4\right)>0\)
\(\lim\limits_{x\rightarrow0,5^+}f\left(x\right)=+\infty;\lim\limits_{x\rightarrow0,5^-}f\left(x\right)=-\infty;\lim\limits_{x\rightarrow2^-}f\left(x\right)=-\infty;\lim\limits_{x\rightarrow2^+}f\left(x\right)=+\infty\)
BBT:
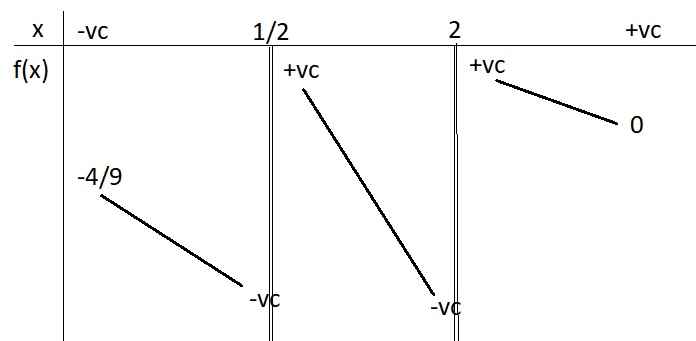
Xét hàm \(g\left(x\right)=x+\left|x-4\right|+a=\left\{{}\begin{matrix}a+4\text{ nếu }x\le4\\2x+a-4\text{ nếu }x\ge4\end{matrix}\right.\)
Từ BBT ta thấy:
- Nếu \(a\ge-3\Rightarrow g\left(x\right)\) cắt f(x) tại 2 điểm phân biệt thỏa mãn \(x< 4\)
- Nếu \(a=-4\Rightarrow g\left(x\right)\) cắt f(x) tại 2 điểm pb thỏa mãn \(x_1< 4< x_2\)
- Nếu \(a\le-5\) \(\Rightarrow g\left(x\right)\) cắt f(x) tại 3 điểm pb thỏa mãn \(x_1< x_2< 4< x_3\) (loại)
Vậy \(a=\left\{-1;-2;-3;-4\right\}\)
AH
Akai Haruma
Giáo viên
29 tháng 4 2023
Lời giải:
Mỗi ngày một lập trình viên hoàn thành:
$1:3:15=\frac{1}{45}$ (công việc)
Sau 1 ngày đầu mọi người hoàn thành:
$\frac{1}{45}\times 15=\frac{1}{3}$ (công việc)
Số công việc còn lại: $1-\frac{1}{3}=\frac{2}{3}$ (công việc)
Số người còn lại: $15-9=6$ (người)
Thời gian để 6 người hoàn thành $\frac{2}{3}$ công việc còn lại:
$\frac{2}{3}: \frac{1}{45}: 6 = 5$ (ngày)
Số ngày mất thêm để hoàn thành công việc:
$5+1-3=3$ (ngày)
c