
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có /2x/= 2x nếu 2x≥0 hay x≥0
= -(2x) nếu 2x<0 hay x<0
Phương trình 2x-2=0 với điều kiện x≥0
Ta có 2x-2=0 <=>2x=2 <=>x=2/2 <=>x=1(thỏa mãn điều kiện)
Phương trình -(2x)-2=0 với điều kiện x<0
Ta có -2x-2=0 <=>-2x=2 <=>x=-1(thỏa mãn điều kiện)
Tập nghiệm phương trình S={1;-1}

a: \(\Leftrightarrow\left(x-2010\right)\left(7x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2010\\x=-\dfrac{1}{7}\end{matrix}\right.\)
b: \(\Leftrightarrow\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
a)7x(x-2010)+(x-2010)=-
(x-2010)(7x+1)=0
x=2010 hoặc x=\(-\dfrac{1}{7}\)
Vậy \(x\in\left\{2010;-\dfrac{1}{7}\right\}\)

a) \(x^2+9x+20=2\sqrt{3x+10}\)
\(\Leftrightarrow\left(x+4\right)^2\left(x+5\right)^2=4\left(3x+10\right)\)
\(\Leftrightarrow x^4+10x^3+25x^2+8x^3+80x^3+200x+16x^2+160x+400=12x+40\)
\(\Leftrightarrow x^4+18x^3+121x^2+360x+400=12x+40\)
\(\Leftrightarrow x^4+18x^2+121x^2+360x+400-12x-40=0\)
\(\Leftrightarrow\left(x^3+15x^2+76x+120\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left(x^2+12x+40\right)\left(x+3\right)=0\)
Nhưng \(x^2+12x+40\ne0\), nên:
\(\Leftrightarrow x+3=0\)
\(\Leftrightarrow x=-3\)
Vậy: nghiệm phương trình là {-3}

3: \(\left(3x+5\right)\left(2x-7\right)\)
\(=6x^2-21x+10x-35\)
\(=6x^2-11x-35\)
4: \(\left(5x-2\right)\left(3x+4\right)\)
\(=15x^2+20x-6x-8\)
\(=15x^2+14x-8\)

e) \(\left(x^2-4\right)\left(x^2+4\right)=\left(x^2\right)^2-4^2=x^4-16\)
f) \(\left(x+y\right)^2+\left(x-y\right)^2=x^2+2xy+y^2+x^2-2xy+y^2=2x^2+2y^2\)
(x2 - 4)(x2 + 4)
Áp dụng hằng đẳng thức số 3, ta có:
<=> \(\left[\left(x^2\right)^2-4^2\right]\)
<=> (x4 - 16)
Mik làm chi tiết rồi, có gì ko hiểu bảo mik

\(a,=\dfrac{2y\left(3x-1\right)^2}{3x^2}\\ b,=\dfrac{\left(3x+2-x-2\right)\left(3x+2+x+2\right)}{x^2\left(x-1\right)}\\ =\dfrac{2x\left(4x+4\right)}{x^2\left(x-1\right)}=\dfrac{8\left(x+1\right)}{x\left(x-1\right)}\\ c,=\dfrac{x^2+3x+4x+12}{x^2+2x+3x+6}\\ =\dfrac{\left(x+3\right)\left(x+4\right)}{\left(x+2\right)\left(x+3\right)}=\dfrac{x+4}{x+2}\)


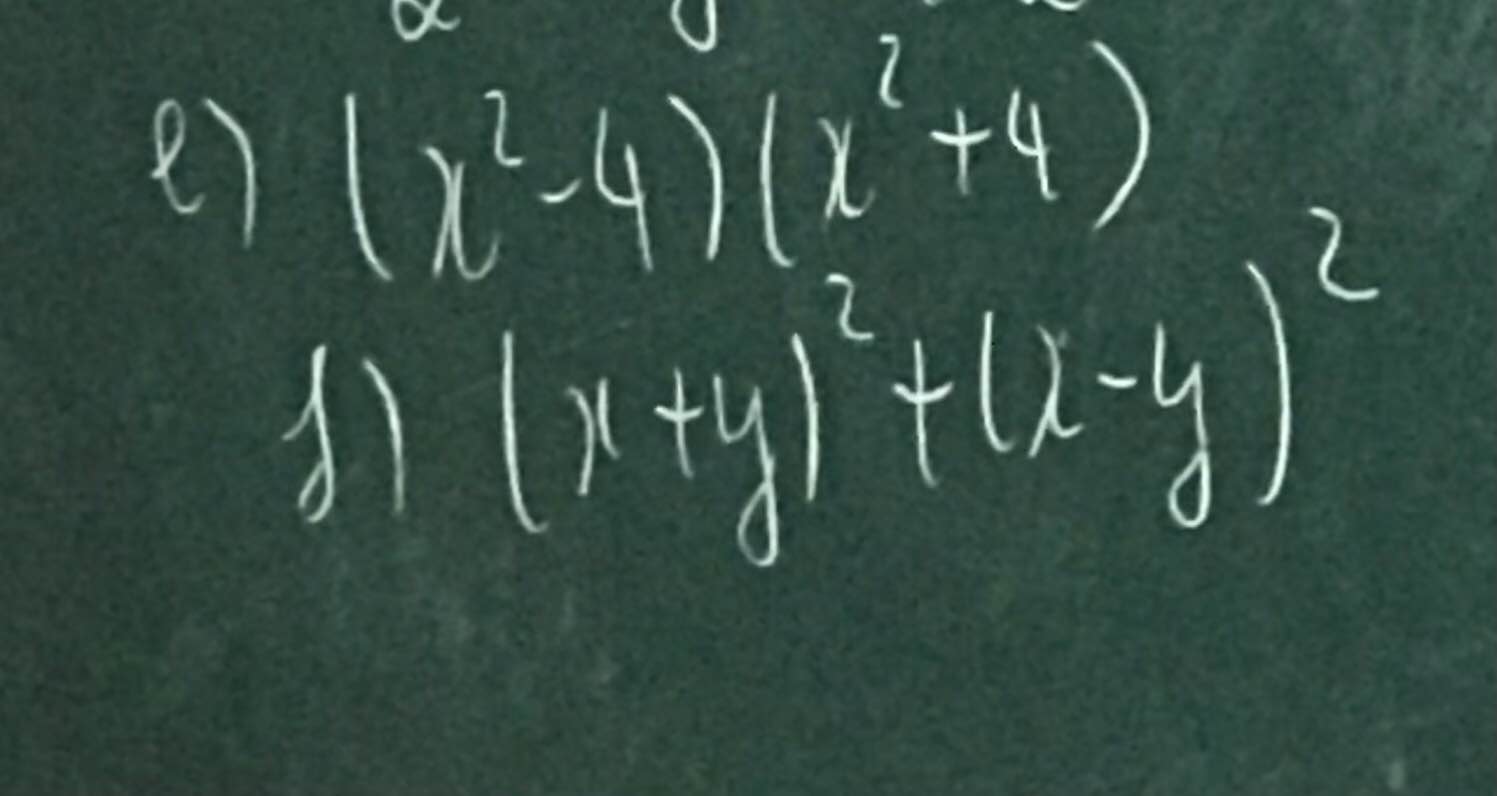
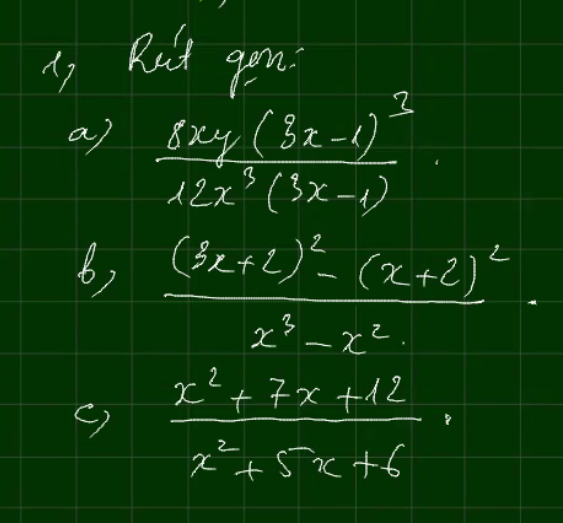
\(7x^2+\left(2x^2+3x^5\right)\)
\(=7x^2+2x^2+3x^5\)
\(=3x^5+9x^2\)