K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
11 tháng 7 2019
6ax2+4ax-9x-6 = 0
<=> ( 6ax2+4ax ) - ( 9x+6 ) = 0
<=> 2ax(3x+2) - 3(3x+2) = 0
<=> ( 2ax-3 )( 3x+2 ) = 0
<=> \(\left[{}\begin{matrix}2ax-3=0\\3x+2=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}2ax=3\\3x=-2\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=\frac{3}{2a}\\x=\frac{-2}{3}\end{matrix}\right.\)
18 tháng 3 2017
Ta co:6ax^2+4ax—9x—6=0
«=»2ax(3x+2)—3(3x+2)=0
«=»(3x+2)(2ax—3)=0
các bục sau tu giai
18 tháng 3 2017
ta có : 6ax2+4ax-9x-6=0
\(\Leftrightarrow\)2ax(3x+2)-3(3x+2)=0
\(\Leftrightarrow\)(3x+2)(2ax-3)=0
xét 3x+2=0\(\Rightarrow\)x=\(\frac{-2}{3}\)
thay x vừa tìm được vào ta tính được a=\(\frac{-13}{3}\)
L
0
TP
1
VC
26 tháng 7 2017
ax(4x2 - 1) - 3(4x2 - 1) = 0
(4x2 - 1) (ax - 3) = 0
4x2 - 1 = 0 => x = + - 1/2
ax - 3 = 0 => a = 3/x
CM
14 tháng 12 2019
Rút gọn biểu thức ta có:
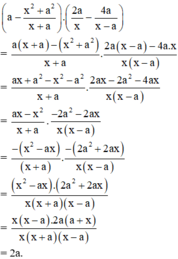
Với a là một số nguyên thì giá trị biểu thức bằng 2a là một số chẵn.
NC
0
9 tháng 2 2022
Bài 2:
a: \(\Leftrightarrow4x^2\left(ax-3\right)-\left(ax-3\right)=0\)
\(\Leftrightarrow\left(ax-3\right)\left(2x-1\right)\left(2x+1\right)=0\)
Trường hợp 1: a=0
=>(2x-1)(2x+1)=0
=>x=1/2 hoặc x=-1/2
Trường hợp 2: a<>0
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-\dfrac{1}{2}\\x=\dfrac{3}{a}\end{matrix}\right.\)
b: \(\Leftrightarrow a^2x^2\left(2x+5\right)-4\left(2x+5\right)=0\)
\(\Leftrightarrow\left(2x+5\right)\left(a^2x^2-4\right)=0\)
Trường hợp 1: a=0
Phương trình sẽ là 2x+5=0
hay x=-5/2
Trường hợp 2: a<>0
Phương trình sẽ là \(\left(2x+5\right)\left[\left(ax\right)^2-4\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{5}{2}\\x=-\dfrac{2}{a}\\x=\dfrac{2}{a}\end{matrix}\right.\)