K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
2
CM
13 tháng 7 2017
a) (x – 45).27 = 0 ó x – 45 = 0 ó x = 45
b) 45.(2x – 4).13 = 0 ó 2x – 4 = 0 ó 2x – 4 = 0 ó 2x = 4 ó x = 2
c) (x – 3).(x – 5) = 0
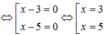
Vậy tập nghiệm của phương trình là S = {3;5}
12 tháng 10 2018
\(2.3^x=10.3^{12}+8.27^4\)
\(\Rightarrow\) \(2.3^x=10.3^{12}+8.3^{12}\)
\(\Rightarrow\) \(2.3^x=3^{12}.\left(10+8\right)\)
\(\Rightarrow\) \(2.3^x=3^{12}.2.9\)
\(\Rightarrow\) \(2.3^x=3^{14}.2\)
\(\Rightarrow\) \(3^x=3^{14}\)
\(\Rightarrow\) \(x=14\)
25 tháng 1 2019
Bài 1:
(x2 - 6)(x2 - 45) < 0
\(\Rightarrow\) x2 - 6, x2 - 45 khác dấu
Mà x2 - 6 > x2 - 45 nên x2 - 6 > 0 và x2 - 45 < 0
\(\Rightarrow\) 6 < x2 < 45
Vì x2 là số chính phương \(\Rightarrow\) x2 \(\in\) {9; 16; 25; 36}
\(\Rightarrow\) x \(\in\) {\(\pm\) 3; \(\pm\)4; \(\pm\)5; \(\pm\)6}
Vậy...
\(\left(45-x\right)\cdot27=0\)
\(\Rightarrow45-x=0:27\)
\(\Rightarrow45-x=0\)
\(\Rightarrow x=45\)