K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
PT
1
CM
23 tháng 1 2017
a) 3 1 5 x − 4 2 3 = 3 1 3 ⇒ 3 1 5 x = 3 1 3 + 4 2 3 = 8 ⇒ x = 8 : 16 5 = 8. 5 16 = 5 2
b) 2 2 3 x + 3 3 4 x = 385 24 ⇒ x 2 2 3 + 3 3 4 = 385 4 ⇒ x . 77 12 = 385 4 ⇒ x = 385 4 : 77 12 = 15
NH
2
18 tháng 12 2021
\(A=4\left(1+4+4^2\right)+...+4^{22}\left(1+4+4^2\right)\)
\(=20\left(1+...+4^{22}\right)⋮20\)
NH
1
PT
1
CM
10 tháng 7 2018
a) 2 5 + 3 5 : 3 5 + − 2 3 − 3 1 2 = 2 5 + 3 5 : − 1 15 = 2 5 − 9 = − 43 5
b) 1 , 25 : 15 20 + 25 % − 5 6 : 4 2 3 = 5 4 . 4 3 + 1 4 − 5 6 : 14 3 = 5 3 + − 7 12 . 3 14 = 37 24
MH
2
25 tháng 12 2021
\(4^{20}+4^{21}+4^{22}+4^{23}=4^{20}\left(1+4+4^2+4^3\right)=4^{20}\cdot85⋮5\left(85⋮5\right)\)
31 tháng 12 2022
A=(4+4^2)+...+4^22(4+4^2)
=20(1+...+4^22) chia hết cho 20
A=4(1+4+4^2)+...+4^22(1+4+4^2)
=21(4+...+4^22) chia hết cho 21
Vì A chia hết cho 20 và 21
và ƯCLN(20;21)=1
nên A chia hết cho 20*21=420
LL
1
AH
Akai Haruma
Giáo viên
2 tháng 1
Lời giải:
$A=(4+4^2)+(4^3+4^4)+...+(4^{23}+4^{24})$
$=(4+4^2)+4^2(4+4^2)+...+4^{22}(4+4^2)$
$=(4+4^2)(1+4^2+....+4^{22})=20(1+4^2+...+4^{22})\vdots 20$
----------------------
$A=(4+4^2+4^3)+(4^4+4^5+4^6)+....+(4^{22}+4^{23}+4^{24})$
$=4(1+4+4^2)+4^4(1+4+4^2)+....+4^{22}(1+4+4^2)$
$=(1+4+4^2)(4+4^4+....+4^{22})=21(4+4^4+...+4^{22})\vdots 21$
--------------------------
Vậy $A\vdots 20; A\vdots 21$. Mà $(20,21)=1$ nên $A\vdots (20.21)$ hay $A\vdots 420$
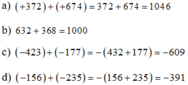
423.177+77.(-423)
=423.177-77.423
=423.(177-77)
=423.100
=42300
tk cho mk nha!
423,177 + 77 . (-423)
= 500,177 . 423
= 211574,871
Hk tốt,
k nhé