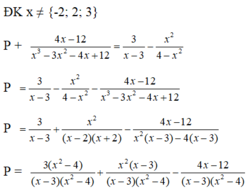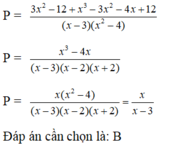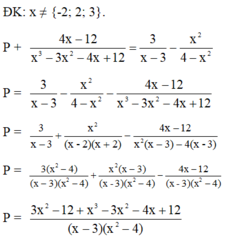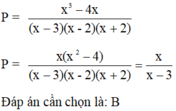K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
24 tháng 1 2019
Điều kiện xác định của phân thức: x ≠ 2
Ta có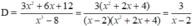 
Với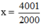 
thỏa mãn điều kiện xác định của phân thức
2 tháng 1 2022
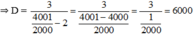
k: \(=\left(2-3x\right)\left(4+6x+9x^2\right)\)
i: \(=3\left(x^2-2xy+y^2\right)=3\left(x-y\right)^2\)
2 tháng 1 2022
\(g,27+27x+9x^2+x^3=\left(3+x\right)^3\\ i,2x^2+2y^2-x^2z+z-y^2z-2=\left(2x^2-x^2z\right)+\left(2y^2-y^2z\right)-\left(2-z\right)=x^2\left(2-z\right)+y^2\left(2-z\right)-\left(2-z\right)=\left(x^2+y^2-1\right)\left(2-z\right)\)
\(k,8-27x^2=2^3-\left(3x\right)^3=\left(2-3x\right)\left(4+6x+9x^2\right)\)
\(l,3x^2-6xy+3y^2=3\left(x^2-2xy+y^2\right)=3\left(x-y\right)^2\)
27 tháng 10 2021
a: \(=\dfrac{35x^3-14x^2+55x^2-22x+35x-14+9}{5x-2}\)
\(=7x^2-11x+7+\dfrac{9}{5x-2}\)
b: \(=\dfrac{\left(2x-3\right)\left(4x^2+6x+9\right)}{2x-3}=4x^2+6x+9\)
HA
1
TP
26 tháng 9 2023
Để đa thức 12x^3 - 7x^2 + a + b chia hết cho đa thức 3x^2 + 2x - 1, ta cần thực hiện phép chia đa thức.
4x - 3
_______________________
3x^2 + 2x - 1 | 12x^3 - 7x^2 + a + b
Để đa thức chia hết cho đa thức 3x^2 + 2x - 1, phần dư phải bằng 0. Vì vậy, ta có:
(12x^3 - 7x^2 + a + b) = (3x^2 + 2x - 1)(4x - 3)
Mở ngoặc, ta có:
12x^3 - 7x^2 + a + b = 12x^3 - 9x^2 + 8x^2 - 6x - 4x + 3
So sánh các hệ số tương ứng, ta có:
-7x^2 + a + b = -9x^2 + 8x^2 - 6x - 4x + 3
Từ đó, ta có hệ phương trình:
-7 = -9 + 8 => 8 = 9 - 7 => 8 = 2
a = -6
b = -4
Vậy, hệ số a = -6 và b = -4 để đa thức 12x^3 - 7x^2 + a + b chia hết cho đa thức 3x^2 + 2x - 1.
K
2
31 tháng 7 2021
a) x4+2x2+1=(x2+1)2
b)=3x2(a+b)+x(a+b)+5(a+b)=(a+b)(3x2+x+5)
c)=x2(a-b)-2x(a-b)-3(a-b)=(a-b)(x2-2x-3)=(a-b)(x-3)(x+1)
d)=2x(y2-a2)-5by(y+a)=(y+a)(2xy-2xa-5by)
31 tháng 7 2021
\(\text{a) x}^4+2x^2+1=\left(x^2+1\right)^2\)
\(\text{b) 3}ax^2+3bx^2+ãx+bx+5a+5b=\left(3ax^2+3bx^2\right) +\left(ax+bx\right)+\left(5a+5b\right)=3x^2+x\left(a+b\right)+5\left(a+b\right)=\left(a+b\right)\left(3x^2+x+5\right)\)
\(\text{c) a}x^2-bx^2-2ax+2bx-3a+3b=\left(\text{a}x^2-bx^2\right)-\left(2ax-2bx\right)-\left(3a-3b\right)=x^2\left(a-b\right)-2x\left(a-b\right)-3\left(a-b\right)=\left(x^2-2x-3\right)\left(a-b\right)\)
24 tháng 9 2021
\(a,=\left(x-1\right)^3\\ b,=\left(1-2x\right)\left(1+2x\right)\\ c,=x^3-8\\ d,=\left(3x-1\right)\left(9x^2+3x+1\right)\\ e,=\left(x+2\right)\left(x^2-2x+4\right)\\ g,=\left(x-2\right)^2\\ h,=x^2-4y^2\\ j,=\left(x-4\right)^2\)