
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: =>2x^2-2x+2x-2-2x^2-x-4x-2=0
=>-5x-4=0
=>x=-4/5
b: =>6x^2-9x+2x-3-6x^2-12x=16
=>-19x=19
=>x=-1
c: =>48x^2-12x-20x+5+3x-48x^2-7+112x=81
=>83x=83
=>x=1

một đòn bẫy dài một mét .đặt ở đâu để có thể dùng 3600n có thể nâng tảng đá nặng 120kg?

2:
=>x^3-1-2x^3-4x^6+4x^6+4x=6
=>-x^3+4x-7=0
=>x=-2,59
4: =>8x-24x^2+2-6x+24x^2-60x-4x+10=-50
=>-62x+12=-50
=>x=1

a: \(=\dfrac{2\left(x+2\right)\left(x-1\right)}{x+2}=2x-2\)
b: \(=\dfrac{2x^3+x^2-6x^2-3x+2x+1}{2x+1}=x^2-3x+1\)
c: \(=\dfrac{x^3+2x^2-2x^2-4x+2x+4}{x+2}=x^2-2x+2\)
d: \(=\dfrac{x^2\left(x-3\right)}{x-3}=x^2\)

b) ( x+ 2) ( 3x-2) - (3x-1) ( x-5) = 11
3x^2 +6x - 2x -4 - 3x^2 +x + 15x -5 =11
20x = 11 +4+5
20x = 20
x=1
c) 2(2x+ 1) ( 8x-3) + ( 3-4x) ( 8x-7) = 6x + 73
(4x + 2)(8x-3) + 24x - 32x^2 -3 +4x = 6x +73
32x^2 + 16x - 12x + 24x - 32x^2 +4x -6x = 73 +6 +3
26x = 82
x= 41/13
a. \(\left(x+2\right)\left(3x-2\right)-\left(3x-1\right)\left(x-5\right)=11\)
\(\Rightarrow3x^2-2x+6x-4-3x^2+15x+x-5=11\)
\(\Rightarrow20x-9=11\)
\(\Rightarrow x=1\)
Vậy..................
b. \(2\left(2x+1\right)\left(8x-3\right)+\left(3-4x\right)\left(8x-7\right)=6x+73\)
\(\Rightarrow\left(4x+2\right)\left(8x-3\right)+\left(3-4x\right)\left(8x-7\right)=6x+73\)
\(\Rightarrow32x^2-12x+16x-6+24x-21-32x^2+28x-6x=73\)
\(\Rightarrow50x-27=73\)
\(\Rightarrow x=100\)
Vậy..............

\(A=-x^2+3x-5\)\(=-\dfrac{11}{4}-\left(x^2-2.\dfrac{3}{2}x+\dfrac{9}{4}\right)=-\dfrac{11}{4}-\left(x-\dfrac{3}{2}\right)^2\le-\dfrac{11}{4}\) với mọi x
\(\Rightarrow A_{max}=-\dfrac{11}{4}\Leftrightarrow x-\dfrac{3}{2}=0\Leftrightarrow x=\dfrac{3}{2}\)
\(B=5x-4x^2-3=-\dfrac{23}{16}-\left(4x^2-2.\dfrac{5}{4}.2x+\dfrac{25}{16}\right)\)\(=-\dfrac{23}{16}-\left(2x-\dfrac{5}{4}\right)^2\)\(\le-\dfrac{23}{16}\forall x\)
\(\Rightarrow B_{max}=-\dfrac{23}{16}\Leftrightarrow2x-\dfrac{5}{4}=0\Leftrightarrow x=\dfrac{5}{8}\)
\(C=5-4x-25x^2=\dfrac{129}{25}-\left(25x^2+2.5x.\dfrac{2}{5}+\dfrac{4}{25}\right)\)\(=\dfrac{129}{25}-\left(5x+\dfrac{2}{5}\right)^2\le\dfrac{129}{25}\forall x\)
\(\Rightarrow C_{max}=\dfrac{129}{25}\Leftrightarrow5x+\dfrac{2}{5}=0\Leftrightarrow x=-\dfrac{2}{25}\)
\(D=3x-2x^2=-2\left(x^2-\dfrac{3}{2}x\right)=-2\left(x^2-2.\dfrac{3}{4}x+\dfrac{9}{16}\right)+\dfrac{9}{8}\)\(=\dfrac{9}{8}-2\left(x-\dfrac{3}{4}\right)^2\le\dfrac{9}{8}\) với mọi x
\(\Rightarrow D_{max}=\dfrac{9}{8}\Leftrightarrow x-\dfrac{3}{4}=0\Leftrightarrow x=\dfrac{3}{4}\)
\(E=2+6x-\dfrac{1}{4}x^2=-\dfrac{1}{4}\left(x^2-24x\right)+2=-\dfrac{1}{4}\left(x^2-2.12x+144\right)+38\)\(=38-\dfrac{1}{4}\left(x-12\right)^2\le38\forall x\)
\(\Rightarrow E_{max}=38\Leftrightarrow x-12=0\Leftrightarrow x=12\)
\(F=-5x^2+4x=-5\left(x^2-\dfrac{4}{5}x\right)=-5\left(x^2-2.\dfrac{2}{5}x+\dfrac{4}{25}\right)+\dfrac{4}{5}\)\(=\dfrac{4}{5}-5\left(x-\dfrac{2}{5}\right)^2\le\dfrac{4}{5}\forall x\)
\(\Rightarrow F_{max}=\dfrac{4}{5}\Leftrightarrow x-\dfrac{2}{5}=0\Leftrightarrow x=\dfrac{2}{5}\)

Ta có : 6x(3x + 5) - 2x(9x - 2) = 17
<=> 18x2 + 30x - 19x2 + 4x = 17
<=> 34x2 = 17
=> x2 = 17 : 34
=> \(x^2=\frac{1}{2}\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{1}{2}\\x=-\frac{1}{2}\end{cases}}\)
\(a,6x\cdot\left(3x+5\right)-2x\cdot\left(9x-2\right)=17\)
\(\Leftrightarrow18x^2+30x-18x^2+4x=17\)
\(\Leftrightarrow34x=17\)
\(\Leftrightarrow x=\frac{1}{2}\)
\(b,2x\cdot\left(3x-1\right)-3x\cdot\left(2x+11\right)-70=0\)
\(\Leftrightarrow6x^2-2x-6x^2-33x-70=0\)
\(\Leftrightarrow-35x=70\)
\(\Leftrightarrow x=-2\)
Đầu bài ý c là j vậy ... mình k thấy zõ
Chúc bạn học giỏi
Kết bạn với mình nha

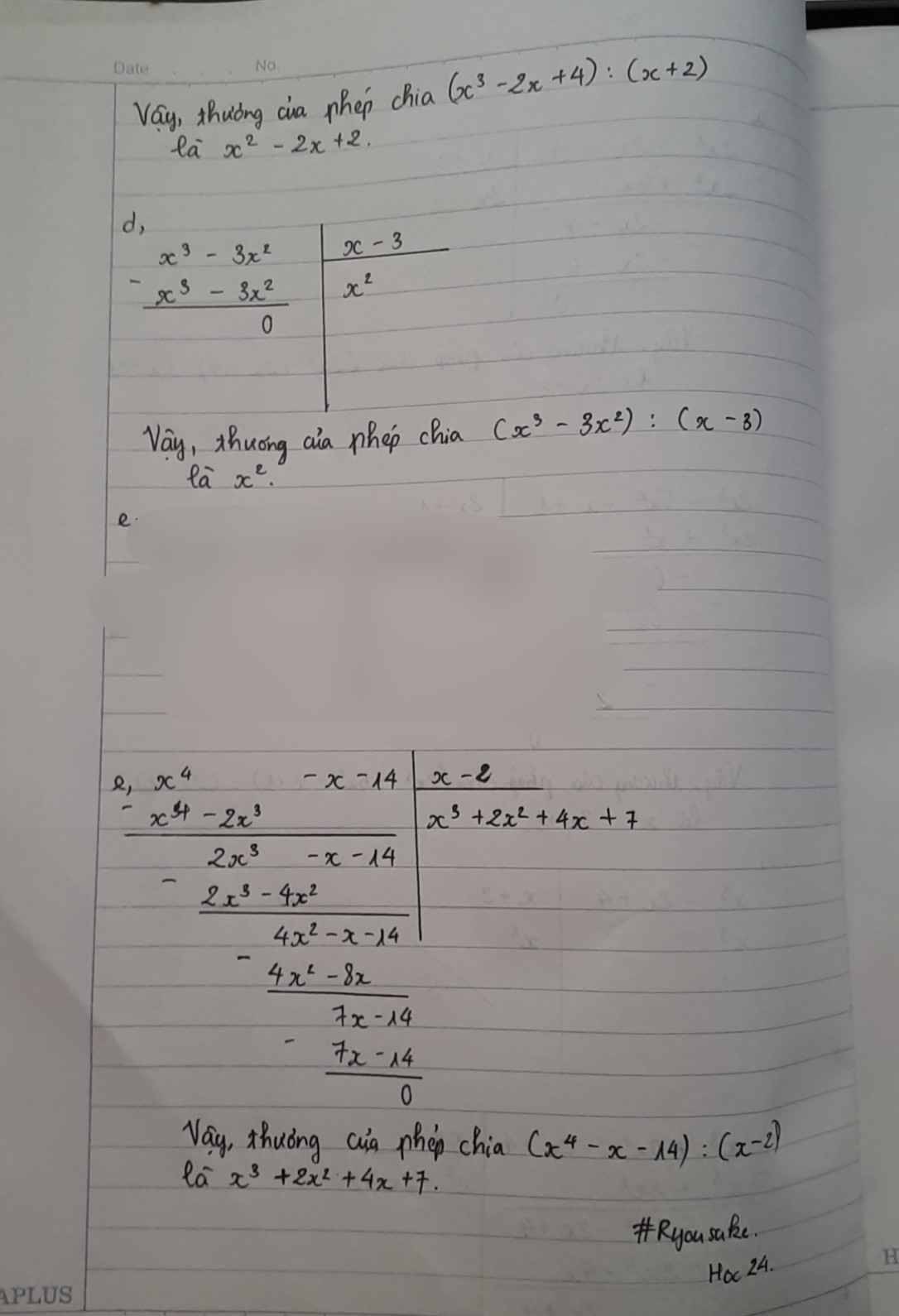

Gúp mik vs