K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
19 tháng 3 2017
\(B=\dfrac{2}{1.4}+\dfrac{2}{4.7}+\dfrac{2}{7.10}+...+\dfrac{2}{97.100}\)
\(B=\dfrac{2}{3}\left(\dfrac{3}{1.4}+\dfrac{3}{4.7}+\dfrac{3}{7.10}+...+\dfrac{3}{97.100}\right)\)
\(B=\dfrac{2}{3}\left(\dfrac{4-1}{1.4}+\dfrac{7-4}{4.7}+\dfrac{10-7}{7.10}+...+\dfrac{100-97}{97.100}\right)\)
\(B=\dfrac{2}{3}\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{97}-\dfrac{1}{100}\right)\)
\(B=\dfrac{2}{3}\left(1-\dfrac{1}{100}\right)\)
\(B=\dfrac{2}{3}.\dfrac{99}{100}\)
\(B=\dfrac{33}{50}\)
US
5
1 tháng 5 2016
\(\frac{5}{1.4}+\frac{5}{4.7}+................+\frac{5}{100.103}\)
\(\frac{1}{3}.\left(5-\frac{5}{4}+\frac{5}{4}-\frac{5}{7}+..............+\frac{5}{100}-\frac{5}{103}\right)\)
\(\frac{1}{3}.\left(5-\frac{5}{103}\right)\)
\(\frac{1}{3}.\left(\frac{510}{103}\right)=\frac{170}{103}\)
1 tháng 5 2016
\(=\frac{5}{3}.\left(\frac{3}{1.4}+\frac{3}{4.7}+...+\frac{3}{100.103}\right)\)
\(=\frac{5}{3}.\left(\frac{1}{1}-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+...+\frac{1}{100}-\frac{1}{103}\right)\)
\(=\frac{5}{3}.\left(\frac{1}{1}-\frac{1}{103}\right)=\frac{5}{3}.\frac{102}{103}=\frac{....}{....}\)
FT
12 tháng 10 2017
\(A=4.4^1.4^3.4^5.....4^{57}=4^{1+3+5+...+57}=4^{\left[\left(\dfrac{57-1}{2}\right)+1\right]:2\left(57+1\right)}=4^{841}\)\(B=3+3^2+3^3+3^4+...+3^{100}\)
\(3B=3\left(3+3^2+3^3+3^4+...+3^{100}\right)\)
\(3B=3^2+3^3+3^4+3^5+...+3^{101}\)
\(3B-B=\left(3^2+3^3+3^4+3^5+...+3^{101}\right)-\left(3+3^2+3^3+3^4....+...+3^{100}\right)\)
\(2B=3^{101}-3\Leftrightarrow B=\dfrac{3^{101}-3}{2}\)
2)
Từ \(1\rightarrow9\) có: \(\left(9-1\right):1+1=9\)(chữ số)
Từ \(10\rightarrow99\) có:\(2\left[\left(99-10\right):1+1\right]=180\)(chữ số)
Từ \(100\rightarrow386\) có:\(3\left[\left(386-100\right):1+1\right]=816\)(chữ số)
Như vậy,Để đánh số trang từ \(1\rightarrow386\) thì cần:
\(9+180+816=1005\)(chữ số)
PT
1
CM
12 tháng 12 2019
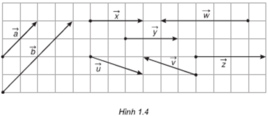
– Các vectơ cùng phương:
a→ và b→ cùng phương
u→ và v→ cùng phương
x→, y→, w→ và z→ cùng phương.
– Các vectơ cùng hướng:
a→ và b→ cùng hướng
x→, y→ và z→ cùng hướng
– Các vectơ ngược hướng:
u→ và v→ ngược hướng
w→ ngược hướng với các vec tơ x→, y→ và z→
– Các vectơ bằng nhau: x→ = y→
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 1 2021
\(\left(3^x;3^y;3^z\right)=\left(a;b;c\right)\Rightarrow\left\{{}\begin{matrix}a;b;c>0\\ab+bc+ca=abc\end{matrix}\right.\)
BĐT cần chứng minh trở thành:
\(\dfrac{a^2}{a+bc}+\dfrac{b^2}{b+ca}+\dfrac{c^2}{c+ab}\ge\dfrac{a+b+c}{4}\)
Thật vậy, ta có:
\(VT=\dfrac{a^3}{a^2+abc}+\dfrac{b^3}{b^2+abc}+\dfrac{c^3}{c^2+abc}\)
\(VT=\dfrac{a^3}{\left(a+b\right)\left(a+c\right)}+\dfrac{b^3}{\left(a+b\right)\left(b+c\right)}+\dfrac{c^3}{\left(a+c\right)\left(b+c\right)}\)
Áp dụng AM-GM:
\(\dfrac{a^3}{\left(a+b\right)\left(a+c\right)}+\dfrac{a+b}{8}+\dfrac{a+c}{8}\ge\dfrac{3a}{4}\)
Làm tương tự với 2 số hạng còn lại, cộng vế với vế rồi rút gọn, ta sẽ có đpcm
29 tháng 9 2017
theo công thức (n-1)n(n+1)=n\(^3\)-n
\(\Rightarrow\) n\(^3\)=n+(n-1)n(n-1)
Ta có :
\(A=1^3+2^3+.....+100^3\)
\(\Rightarrow1+2+1\cdot2\cdot3+3+2\cdot3\cdot4+100+99\cdot100\cdot101\)\(=\left(1+2+3+...+100\right)+\left(1\cdot2\cdot3+2\cdot3\cdot4+...+99\cdot100\cdot101\right)\) =5050+101989800
=101994850
Chào bạn, bạn hãy theo dõi bài giải của mình nhé!
\(\frac{3}{1\cdot4}+\frac{3}{4\cdot7}+\frac{3}{7\cdot10}+...+\frac{3}{97\cdot100}\)
\(=1-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+\frac{1}{7}-\frac{1}{10}+...+\frac{1}{97}-\frac{1}{100}\)
\(=1-\frac{1}{100}=\frac{100}{100}-\frac{1}{100}=\frac{99}{100}\)
Chúc bạn học tốt!