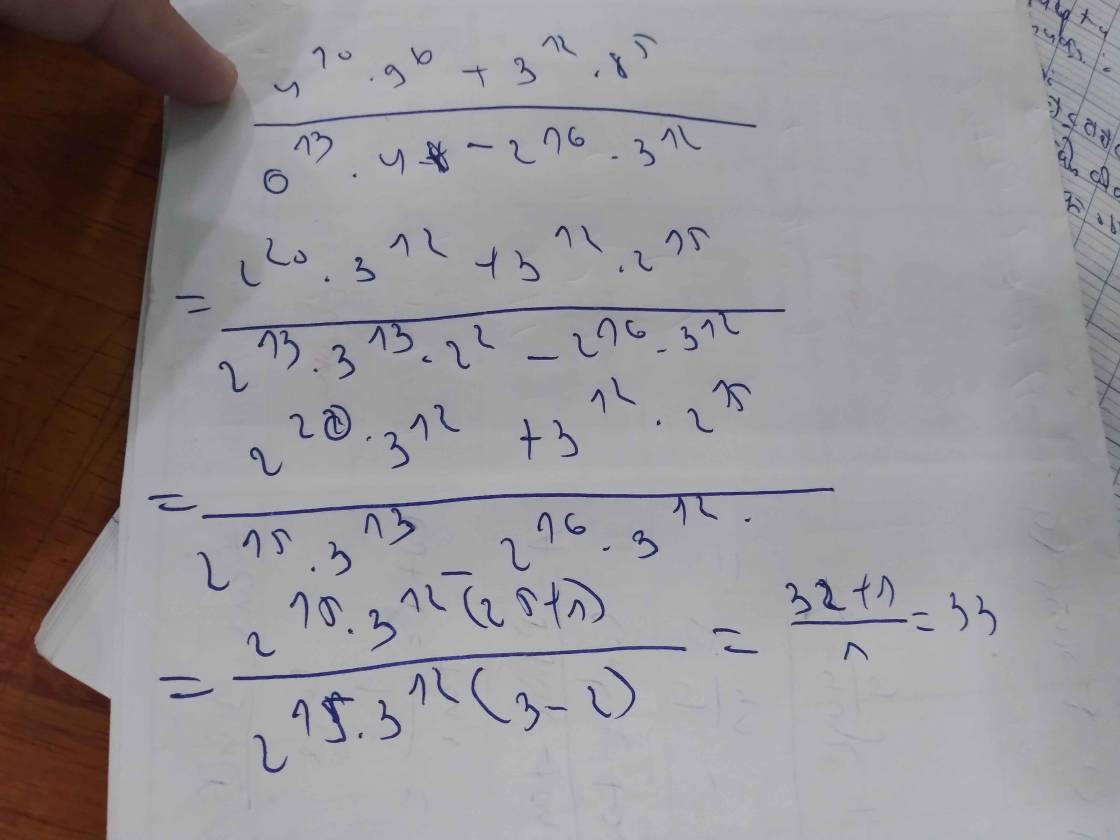Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta có: 100334 = (102)334 = 10668
1000300= (103)300= 10900
=> 10668 < 10900
=> 100334 < 1000300
Ta có:
100334 = ( 102)334= 10 668
1000300 = (103) 300= 10900
Ta có: 10668 < 10900
=> 100 334< 1000300

\(B=7+7^2+...+7^{100}\)
\(B=\left(7+7^2\right)+...+\left(7^{99}+7^{100}\right)\)
\(B=7\left(1+7\right)+...+7^{99}\left(1+7\right)\)
\(B=7\cdot8+...+7^{99}\cdot8\)
\(B=8\cdot\left(7+...+7^{99}\right)⋮8\left(đpcm\right)\)
\(B=7+7^2+7^3+...+7^{100}\)
\(B=\left(7+7^2+7^3\right)+...+\left(7^{98}+7^{99}+7^{100}\right)\)
\(B=399\cdot1+...+7^{97}\cdot\left(7+7^2+7^3\right)\)
\(B=399\cdot1+...+7^{97}\cdot399\)
\(B=399\cdot\left(1+...+7^{97}\right)⋮399\left(đpcm\right)\)




\(A=1-2+3-4+5-6+7-8+...+99-100\)
\(A=\left(-1\right)+\left(-1\right)+\left(-1\right)+\left(-1\right)+...+\left(-1\right)\)
\(A=\left(-1\right).50\)
\(A=-50\)
\(B=1+3-5-7+9+11-...-397-399\)
\(B=1-2+2-2+2-...+2-2-399\)
\(B=1-399\)
\(B=-398\)
\(C=1-2-3+4+5-6-7+...+97-98-99+100\)
\(C=-1+1-1+1-...-1+1\)
\(C=0\)
\(D=2^{2024}-2^{2023}-...-1\)
\(D=2^{2024}-\left(2^0+2^1+2^2+...2^{2023}\right)\)
\(D=2^{2024}-\left(\dfrac{2^{2024}-1}{2-1}\right)\)
\(D=2^{2024}-\left(2^{2024}-1\right)\)
\(D=2^{2024}-2^{2024}+1\)
\(D=1\)
A = 1 - 2 + 3 - 4 + 5 - 6 + 7 - 8 +...+ 99 - 100
A = (1 - 2) + ( 3 - 4) + ( 5- 6) +....+(99 - 100)
Xét dãy số 1; 3; 5;...;99
Dãy số trên là dãy số cách đều có khoảng cách là: 3 - 1 = 2
Dãy số trên có số số hạng là: (99 - 1) : 2 + 1 = 50 (số)
Vậy tổng A có 50 nhóm, mỗi nhóm có giá trị là: 1- 2 = -1
A = - 1\(\times\)50 = -50
b,
B = 1 + 3 - 5 - 7 + 9 + 11-...- 397 - 399
B = ( 1 + 3 - 5 - 7) + ( 9 + 11 - 13 - 15) + ...+( 393 + 395 - 397 - 399)
B = -8 + (-8) +...+ (-8)
Xét dãy số 1; 9; ...;393
Dãy số trên là dãy số cách đều có khoảng cách là: 9-1 = 8
Dãy số trên có số số hạng là: ( 393 - 1): 8 + 1 = 50 (số hạng)
Tổng B có 50 nhóm mỗi nhóm có giá trị là -8
B = -8 \(\times\) 50 = - 400
c,
C = 1 - 2 - 3 + 4 + 5 - 6 +...+ 97 - 98 - 99 +100
C = ( 1 - 2 - 3 + 4) + ( 5 - 6 - 7+ 8) +...+ ( 97 - 98 - 99 + 100)
C = 0 + 0 + 0 +...+0
C = 0
d, D = 22024 - 22023- ... +2 - 1
2D = 22005- 22004 + 22003+...- 2
2D + D = 22005 - 1
3D = 22005 - 1
D = (22005 - 1): 3

\(A=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{99}}\)
\(\Rightarrow\dfrac{A}{3}=\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{100}}\)
\(\Rightarrow A-\dfrac{A}{3}=\dfrac{2A}{3}=\left(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}\right)-\left(\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{100}}\right)\)
\(\Rightarrow\dfrac{2A}{3}=\left(\dfrac{1}{3^2}-\dfrac{1}{3^2}\right)+\left(\dfrac{1}{3^3}-\dfrac{1}{3^3}\right)+...+\left(\dfrac{1}{3^{99}}-\dfrac{1}{3^{99}}\right)+\left(\dfrac{1}{3}-\dfrac{1}{3^{100}}\right)=\dfrac{1}{3}-\dfrac{1}{3^{100}}\)
\(\Rightarrow2A=3\cdot\left(\dfrac{1}{3}-\dfrac{1}{3^{100}}\right)\)
\(\Rightarrow\text{A}=\dfrac{1-\dfrac{1}{3^{99}}}{2}\)
\(\Rightarrow A=\dfrac{1}{2}-\dfrac{1}{2.3^{99}}< \dfrac{1}{2}\)

1: \(=\left(217-213+186\right)+\left(-14-49+54\right)\)
\(=190-9=181\)
2: \(=-38\cdot25+38\cdot4-25\cdot4+25\cdot38\)
\(=13\cdot4=52\)
3: \(=-39\cdot5+39\cdot99+99\cdot10-99\cdot39\)
\(=-195+990=795\)
4: =(1+3-5-7)+(9+11-13-15)+...+(393+395-397-399)
=(-8)+(-8)+...+(-8)
=-800

`#3107.101107`
\(\dfrac{4^{10}\cdot9^6+3^{12}\cdot8^5}{6^{13}\cdot4-2^{16}\cdot3^{12}}\)
\(=\dfrac{2^{20}\cdot3^{12}+3^{12}\cdot2^{15}}{2^{13}\cdot3^{13}\cdot2^2-2^{16}\cdot3^{12}}\)
\(=\dfrac{3^{12}\cdot\left(2^{20}+2^{15}\right)}{3^{12}\cdot\left(2^{15}\cdot3-2^{16}\right)}\)
\(=\dfrac{2^{20}+2^{15}}{2^{15}\cdot3-2^{16}}\)
\(=\dfrac{2^{15}\cdot\left(2^5+1\right)}{2^{15}\cdot\left(3-2\right)}\)
\(=\dfrac{32+1}{1}\)
\(=33\)

Ta có :
Vì số \(2^{323}\) và \(3^{323}\) có số mũ bằng nhau ⇒ Ta so sánh phần cơ số
Vì \(2< 3\Rightarrow2^{323}< 3^{323}\)
Vậy \(2^{323}< 3^{323}\)