Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x,y,z là số tiền thưởng của ba công nhân lần lượt (x,y,z > 0)
Gỉa sử x,y,z tỉ lệ thuận với 3;4;7 ta có: x 3 = y 5 = z 7 và x+ y = 5,6
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
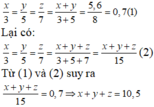
Tổng số tiền thưởng của ba người là 10,5 triệu
Đáp án cần chọn là C

a) Gọi số tiền thưởng của ba người lần lượt là a,b,c(triệu đồng)
Theo điều kiện của bài ta có : \(a:b:c=3:5:7\)hoặc \(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}\)và a + b = 5,6
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b}{3+5}=\frac{5,6}{8}=0,7\)
=> \(\hept{\begin{cases}\frac{a}{3}=0,7\\\frac{b}{5}=0,7\\\frac{c}{7}=0,7\end{cases}}\Rightarrow\hept{\begin{cases}a=2,1\\b=3,5\\c=4,9\end{cases}}\)
=> \(a+b+c=2,1+3,5+4,9=10,5\)
Vậy tổng số tiền của ba người được thưởng là 10,5 triệu đồng
Còn câu b bạn tự làm đi nhé

Giải:
Gọi số tiền thưởng của 3 người lần lượt là a, b, c ( a,b,c thuộc N* )
Ta có:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}\) và \(a+b=5600000\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b}{3+5}=\frac{5600000}{8}=700000\)
+) \(\frac{a}{3}=700000\Rightarrow a=2100000\)
+) \(\frac{b}{5}=700000\Rightarrow b=3500000\)
+) \(\frac{c}{7}=700000\Rightarrow c=4900000\)
Vậy người thứ nhất được 2100000 đồng ( 2.1 triệu )
người thứ 2 được 3500000 đồng ( 3.5 triệu )
người thứ 3 được 4900000 đồng ( 4.9 triệu )
Gọi tiền thưởng của 3 người lần lượt là a,b,c (triệu)(a,b,c>0).
Tổng số tiền thưởng của người 1 và người 2 là 5,6 triệu đồng nên a+b=5,6
Số tiền thưởng tỉ lệ thuận với năng suất lao động nên:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b}{3+5}=\frac{5,6}{8}=0,7\)
\(\Rightarrow a=0,7.3=2,1\) ;\(b=0,7.5=3.5\) ;\(c=0,7.7\) =4,9
Do đó tổng tiền thưởng của 3ng là:2,1+3,5+4,9=10,5(tr).

Gọi tiền thưởng của 3 người lần lượt là a,b,c (triệu)(a,b,c>0).
Tổng số tiền thưởng của ng1 và ng2 là 5,6 triệu đồng nên a+b=5,6
Số tiền thưởng tỉ lệ thuận với năng suất lao động nên: a3=b5=c7=a+b3+5=5,68=0,7.
⇒a=0,7.3=2,1(tr);b=0,7.5=3,5(tr);c=0,7.7=4,9(tr).
Do đó tổng tiền thưởng của 3ng là:2,1+3,5+4,9=10,5(tr).
Nếu đúng thì tích mình nha bạn

gọi năng suất của 3 công nhân đó là x,y,z ta có
x/3=y/5=z/7 và x+y=5,6 (triệu)
Áp dụng tính chất dãy tỉ số bằng nhau ta có
x/3=y/5=z/7=x+y/3+5=5,6/8=0,7
với x/3=0,7=>x=2,1(triệu)
với y/5=0,7=>y=3,5(triệu)
với z/7=0.7=>z=4.9(triệu)
KL............

Gọi số tiền của 3 người thợ lần lượt là x,y,z
Vì số tiền thưởng và năng suất lao động là 2 đại lượng tỉ lệ thuận nên
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{7}\)
Theo tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{z}{7}=\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z-x}{7-3}=\dfrac{200000}{4}=50000\)
\(\Rightarrow x=50000.3=150000\)
\(y=50000.5=250000\)
\(z=50000.7=350000\)
Số tiền thưởng của 3 người thợ lần lượt là 150000,250000,350000 ( đồng )

1.Gọi độ dài 3 cạnh của tam giác lần lượt là a,b,c (a<b<c;a,b,c>0
a,Theo đề bài ta có:\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a+b+c}{3+5+7}=\dfrac{45}{15}=3\)
\(\dfrac{a}{3}=3=>a=9\left(cm\right)\)
\(\dfrac{b}{5}=3=>b=15\left(cm\right)\)
\(\dfrac{c}{7}=3=>c=21\left(cm\right)\)
Vậy độ dài 3 cạnh của tam giác là: 9 cm; 15 cm ; 21 cm
b,Theo đề bài ta có:\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{c+a-b}{7+3-5}=\dfrac{20}{5}=4\)
\(\dfrac{a}{3}=4=>a=12\left(cm\right)\)
\(\dfrac{b}{5}=4=>b=20\left(cm\right)\)\(\dfrac{c}{7}=4=>c=28\left(cm\right)\)
Vậy độ dài 3 cạnh tam giác là:12 cm; 20 cm ; 28 cm
2.Tương tự như vậy bn nhé!![]()
