Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

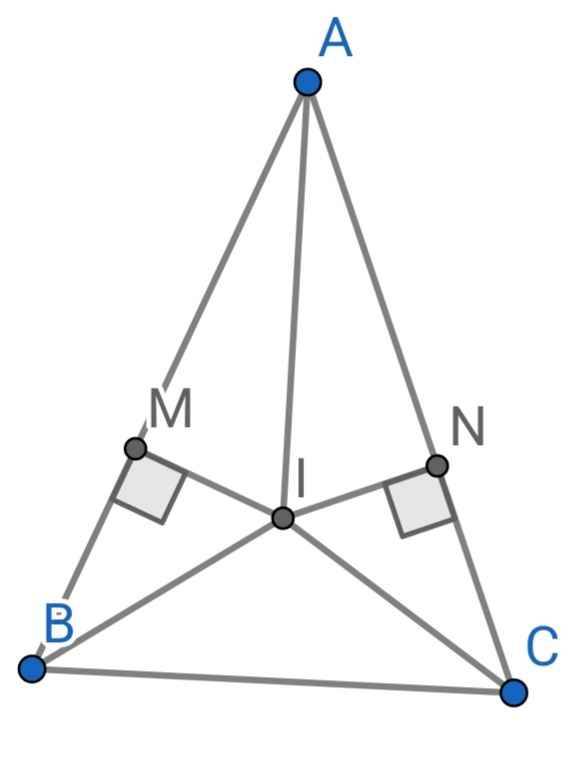 Do I là giao điểm của hai đường phân giác BI và CI của ∆ABC
Do I là giao điểm của hai đường phân giác BI và CI của ∆ABC
⇒ AI là đường phân giác của ∆ABC
⇒ ∠MAI = ∠NAI
Xét hai tam giác vuông: ∆AMI và ∆ANI có:
AI là cạnh chung
∠MAI = ∠NAI (cmt)
⇒ AMI = ANI (cạnh huyền - góc nhọn)
⇒ IM = IN (hai cạnh tương ứng)
Hình b tự vẽ nhé
Kẻ IK vuông góc BC
Xét △BMI và △BKI, ta có
Góc BMI= góc BKI = 90o
Góc MBI= góc IBK ( BI là phân giác góc ABC)
BI cạnh chung
=> △BMI= △BKI (ch-gn)
=> IM= IK ( 2 cạnh tương ứng)
CMTT=> △CNI= △CKI
=> IN=IK
=> IM=IN

Sửa đề: Vuông góc với AC,AP tại N,P
a: Xét ΔBPI vuông tại P và ΔBMI vuông tại M có
BI chung
\(\widehat{PBI}=\widehat{MBI}\)
Do đó: ΔBPI=ΔBMI
=>BP=BM
b: Xét ΔIMC vuông tại M và ΔINC vuông tại N có
CI chung
\(\widehat{MCI}=\widehat{NCI}\)
Do đó: ΔIMC=ΔINC
=>IM=IN
c: ΔMCI=ΔNCI
=>MC=CN
BP+CN
=BM+MC
=BC
d: ΔBPI=ΔBMI
=>IP=IM
mà IM=IN
nên IP=IN
Xét ΔAPI vuông tại P và ΔANI vuông tại N có
AI chung
IP=IN
Do đó: ΔAPI=ΔANI
=>\(\widehat{PAI}=\widehat{NAI}\)
=>AI là phân giác của \(\widehat{BAC}\)

Xét ΔAMI vuông tại M và ΔAPI vuông tại P có
AI chung
\(\widehat{MAI}=\widehat{PAI}\)
Do đó: ΔAMI=ΔAPI
Suy ra: IM=IP(1)
Xét ΔINC vuông tại N và ΔIPC vuông tại P có
IC chung
\(\widehat{NCI}=\widehat{PCI}\)
Do đó: ΔINC=ΔIPC
Suy ra: IN=IP(2)
Từ (1) và (2) suy ra IM=IN=IP

a) Ta thấy \(\widehat{B}+\widehat{C}=180^o-60^o=120^o\)
\(\Rightarrow\widehat{IBC}+\widehat{ICB}=\frac{\widehat{B}+\widehat{C}}{2}=60^o\)
Vậy thì \(\widehat{BIC}=180^o-\widehat{IBC}-\widehat{ICB}=120^o\)
b) Ta có ngay \(\widehat{EIB}=\widehat{IBC}+\widehat{ICB}=60^o=\widehat{BIN}\)
Vậy thì \(\Delta EBI=\Delta NBI\left(g-c-g\right)\Rightarrow IE=IN\)
Tương tự ID = IN nên IE = IN = ID.
a, Trong tam giác ABC có : góc ABC + góc ACB + góc BAC = 180 độ
=> góc ABC + góc ACB =180 độ - góc BAC = 180 độ - 60 độ = 120 độ
Mà BD và CE lần lượt là phân giác của góc ABC ; ACB nên
120 độ = 2.góc IBC + 2.góc ICB = 2.(góc IBC + góc ICB)
=> góc IBC + góc ICB = 120 độ : 2 = 60 độ
Trong tam giác IBC có : góc IBC + góc ICB + góc BIC = 180 độ
=> góc BIC = 180 độ - (góc IBC + góc ICB) = 180 độ - 60 độ = 120 độ

a) tự xét tam giác zuông ABD = tam giác zuông MBD( cạnh huyền - góc nhọn )
=>AB=AM
=> Tam giác ABM cân
b)Tự xét tam giácAEC= ENC
=>CN=CA
khi đó AB+AC=BM+CN
=> BM+MC+MN=BC+MN
=>MN=AB+BC-BC
c) tam giác AMB cân
=> góc AMB =\(\frac{180^0-\widehat{ABC}}{2}=90^0-\frac{\widehat{ABC}}{2}\)
từ ANC cân ở N ( tự cm)
=> góc ANB =180-góc ACB /2=90 độ -ACB/2
trong tám giác AMN có
\(\widehat{MAN}=180^0-\widehat{AMB}-\widehat{ANC=180^0-\left(90^0-\frac{\widehat{ABC}}{2}\right)-\left(90^0-\frac{\widehat{ACB}}{2}\right)}\)
=>\(\widehat{\widehat{MAN}=\frac{\widehat{ABC}}{2}+\frac{ACB}{2}=\frac{90}{2}=45^0}\)
zì tam giác ABC zuông tại A nên góc ABC +ACB=90 độ
d) zì tam giac AMB cân ở B nên đường phân giác BD đồng thời là đường cao
=>BD\(\perp AM\)hay \(GI\perp AK\)
Mặt khác tam giác ANC cân ở C ( cái này cậu tự cm ở trên mình bảo ấy )
do đó đường phân giác CE đồng thời là đường cao
=>\(CE\perp AN=>KI\perp AG\)
trong tam giác AKG có 2 đường cao xuất phát từ G , K cắt nhau tại I
=> I là trực tâm của tam giác AKG
=>\(AI\perp GK\)ở H nên góc AHG=90 độ
a: Xét ΔBNI vuông tại N và ΔBMI vuông tại M có
BI chung
\(\widehat{NBI}=\widehat{MBI}\)(BI là phân giác của góc ABC)
Do đó: ΔBNI=ΔBMI
=>IN=IM
Xét ΔCNI vuông tại N và ΔCPI vuông tại D có
CI chung
\(\widehat{NCI}=\widehat{PCI}\)
Do đó: ΔCNI=ΔCPI
=>IN=IP
=>IM=IN=IP
b: Xét ΔAMI vuông tại M và ΔAPI vuông tại P có
AI chung
IM=IP
Do đó: ΔAMI=ΔAPI
=>\(\widehat{MAI}=\widehat{PAI}\)
=>\(\widehat{BAI}=\widehat{CAI}\)
=>AI là phân giác của góc BAC