Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi độ dài các cạnh của tam giác lần lượt là x, y, z (cm)
Theo đề bài ta có:
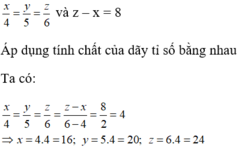
Chọn đáp án A

gọi 3 cạnh của tam giác là a,b,c có:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}\) (trong đó a là cạnh bé nhất, c là cạnh lớn nhất)
ADTCCDTSBN ta có:
\(\frac{a-c}{7-3}=\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=2\)
\(\hept{\begin{cases}\frac{a}{3}=2\\\frac{b}{5}=2\\\frac{c}{7}=2\end{cases}}\)
\(\Rightarrow a=6,b=10,c=14\)
Gọi độ dài của 3 cạnh đó lần lượt là \(a,b,c\)
\(\Rightarrow\frac{a}{3}=\frac{b}{5}=\frac{c}{7}\)
Đặt \(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=k\Rightarrow\hept{\begin{cases}a=3k\\b=5k\\c=7k\end{cases}}\)
Ta thấy \(3k< 5k< 7k\)(k>0 vì độ dài cạnh của tam giác không thể bé hơn hoặc bằng 0)
\(\Rightarrow7k-3k=8\Rightarrow4k=8\Rightarrow k=2\)
\(\Rightarrow\hept{\begin{cases}a=2.3=6\left(cm\right)\\b=2.5=10\left(cm\right)\\c=2.7=14\left(cm\right)\end{cases}}\)
Vậy,.......
HỌC TỐT

\(a,\) Gọi độ dài 3 cạnh là a,b,c(cm;0<a<b<c<120)
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{120}{12}=10\\ \Rightarrow \begin{cases} a=10.3=30\\ b=10.4=40\\ c=10.5=50 \end{cases} \)
Vậy ...
\(b,\) Gọi độ dài 3 cạnh là a,b,c(cm;0<a<b<c)
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{c-a}{7-3}=\dfrac{80}{4}=20\\ \Rightarrow \begin{cases} a=20.3=60\\ b=20.5=100\\ c=20.7=140 \end{cases}\\ \Rightarrow P=a+b+c=300(cm)\)

Gọi 3 cạnh là a ; b ;c
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{c-a}{5-3}=\frac{8}{2}=4\)
a =3.4 =12
b =4.4 =16
c =5.4 =20
Gọi độ dài các cạnh của tam giác đó lần lượt là : x;y;z ( cm )
Theo đề bài ta có :
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\) và z - x = 8
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{z-x}{5-3}=\frac{8}{2}=4\)
\(\frac{x}{3}=4\Rightarrow x=3\cdot4=12\)
\(\frac{y}{4}=4\Rightarrow y=4\cdot4=16\)
\(\frac{z}{5}=4\Rightarrow z=4\cdot5=20\)
Vậy độ dài các cạnh của tam giác đó lần lượt là 12 cm ; 16 cm và 20 cm

Gọi độ dài 3 cạnh của tam giác lần lượt là x, y, z (đơn vị: m)
Ba cạnh tỉ lệ với 3; 4; 5 => \(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\)
Cạnh lớn nhất hơn cạnh nhỏ nhất 6m => z - x = 6.
Theo tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{z-x}{5-3}=\frac{6}{2}=3\)
\(\frac{x}{3}=3\Rightarrow x=3.3=9\)
\(\frac{y}{4}=3\Rightarrow y=3.4=12\)
\(\frac{z}{5}=3\Rightarrow z=3.5=15\)
Vậy, độ dài mỗi cạnh của tam giác lần lượt là 9; 12; 15 (m)
@Nghệ Mạt
#cua

Gọi a(m); b(m) và c(m) lần lượt là độ dài ba cạnh của tam giác(Điều kiện: a>0; b>0; c>0 và a<b<c)
Vì độ dài ba cạnh tỉ lệ với 3;4;5 nên a:b:c=3:4:5
hay \(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\)
Vì cạnh lớn nhất dài hơn cạnh nhỏ nhất là 6m nên c-a=6
Áp dụng tính chất của dãy tĩ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{c-a}{5-3}=\dfrac{6}{2}=3\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{a}{3}=3\\\dfrac{b}{4}=3\\\dfrac{c}{5}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=9\left(nhận\right)\\b=12\left(nhận\right)\\c=15\left(nhận\right)\end{matrix}\right.\)
Vậy: Độ dài ba cạnh của tam giác đó lần lượt là 9m; 12m và 15m

Gọi độ dài của các cạnh tam giác là a, b, c tỉ lệ với 3, 4, 5
Theo bài ra ta có:
\(a:b:c=3:4:5\) và c - a = 6
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{c-a}{5-3}=\dfrac{6}{2}=3\)
Do đó: \(\Rightarrow\left\{{}\begin{matrix}3.3=9\\4.3=12\\5.3=15\end{matrix}\right.\)
Vậy:...
Gọi độ dài các cạch của tam giác là a,b,c với các cạnh là 3,4,5
Theo đề ta có:
a:b:c=3:4:5 và c-a =6
Áp dụng tính chất của dãy số bangừ nhau ta có:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{c-a}{5-3}=\dfrac{6}{2}=3\)
Vậy ta có như sau:
\(\dfrac{a}{3}=3\Rightarrow a=9\)
\(\dfrac{b}{4}=3\Rightarrow b=12\)
\(\dfrac{c}{5}=3\Rightarrow c=15\)