K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TV
0
PT
1
CM
10 tháng 4 2019
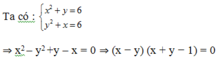
- Khi x = y thì x 2 + x - 6 = 0 ⇔ x = - 3 ; x = 2
- Khi y = 1 - x thì x 2 + 1 - x - 6 = 0 ⇔ x 2 - x - 5 = 0 ⇔ x 1 , 2 = 1 ± 21 2
Vậy hệ phương trình đã cho có 4 nghiệm (−3; −3), (2; 2), 1 + 21 2 ; 1 − 21 2 và 1 − 21 2 ; 1 + 21 2
Đáp án cần chọn là: B
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 3 2020
ĐKXĐ: ...
\(\sqrt{12y-x^2y}=12-x\sqrt{12-y}\)
\(\Rightarrow12y-x^2y=144+12x^2-x^2y-24x\sqrt{12-y}\)
\(\Leftrightarrow x^2-2x\sqrt{12-y}+12-y=0\)
\(\Leftrightarrow\left(x-\sqrt{12-y}\right)^2=0\Rightarrow x=\sqrt{12-y}\)
\(\Rightarrow y=12-x^2\)
Thay vào pt (1):
\(3x^2-x+3=\sqrt{3x+1}+\sqrt{5x+4}\)
\(\Leftrightarrow3x^2-3x+\left(x+1-\sqrt{3x+1}\right)+\left(x+2-\sqrt{5x+4}\right)=0\)
\(\Leftrightarrow3\left(x^2-x\right)+\frac{x^2-x}{x+1+\sqrt{3x+1}}+\frac{x^2-x}{x+2+\sqrt{5x+4}}=0\)
\(\Leftrightarrow...\)
PT
1
CM
5 tháng 5 2017
Điều kiện: x , y ≥ 1
Ta có: 2 x + y − 1 = 1 2 y + x − 1 = 1 ⇒ 2 x − 2 y + y − 1 − x − 1 = 0
⇒ 2 x − y + y − x y − 1 + x − 1 = 0 ⇒ x − y 2 − 1 y − 1 + x − 1 = 0
Khi x = y thì 2 x + x + 1 = 1 ⇒ x + 1 = 1 − 2 x (vô nghiệm do x ≥ 1 thì V T ≥ 0 , V P < 0 )
Khi y − 1 + x − 1 = 1 2 thì 2 x + 2 y + 1 2 = 2 ⇒ x + y = 3 4 (vô nghiệm vì x , y ≥ 1 )
Vậy hệ phương trình vô nghiệm
Đáp án cần chọn là: B
LB
1
14 tháng 12 2021
\(PT\left(2\right)\Leftrightarrow x=y-1\\ PT\left(1\right)\Leftrightarrow2\left(y-1\right)^2+y\left(1-y\right)+3y^2=7\left(y-1\right)+12y-1\\ \Leftrightarrow2y^2-11y+5=0\\ \Leftrightarrow\left[{}\begin{matrix}y=5\Leftrightarrow x=4\\y=\dfrac{1}{2}\Leftrightarrow x=-\dfrac{1}{2}\end{matrix}\right.\)
Vậy ...
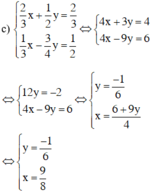
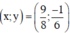
Ta có: \(2y^3-6y^2+12y-8\)
\(=2\left(y^3-3y^2+6y-4\right)\)
\(=2\left(y^3-y^2-2y^2+2y+4y-4\right)\)
\(=2\left(y-1\right)\left(y^2-2y+4\right)\)
\(2y^3-6y^2+12y-8=2y^3-4y^2-2y^2+8y+4y-8\)
\(=\left(2y^3-4y^2+8y\right)-\left(2y^2-4y+8\right)\)
\(=\left(2y^2-4y+8\right)y-\left(2y^2-4y+8\right)\)
\(=\left(y-1\right)\left(2y^2-4y+8\right)\)
\(=2\left(y-1\right)\left(y^2-2y+4\right)\)