K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 5 2021
1,\(K=\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{x}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{6-2\sqrt{5}}+\sqrt{6+2\sqrt{5}}\right)\)\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{5}-1\right)^2}+\sqrt{\left(\sqrt{5}+1\right)^2}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\left|\sqrt{5}-1\right|+\sqrt{5}+1\right)\)\(=\dfrac{1}{\sqrt{2}}\left|\sqrt{5}-1+\sqrt{5}+1\right|=\dfrac{1}{\sqrt{2}}.2\sqrt{5}\)\(=\sqrt{10}\)
2, \(\sqrt{x-3}-2\sqrt{x^2-3x}=0\left(đk:x\ge3\right)\)
\(\Leftrightarrow\sqrt{x-3}\left(1-2\sqrt{x}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-3}=0\\1-2\sqrt{x}=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\left(ktm\right)\end{matrix}\right.\)
Vậy pt có nghiệm x=3
3, \(\dfrac{9x-7}{\sqrt{7x+5}}=\sqrt{7x+5}\left(đk:x>-\dfrac{5}{7}\right)\)
\(\Leftrightarrow9x-7=7x+5\)
\(\Leftrightarrow x=6\left(tm\right)\)
4, \(x-5\sqrt{x}+4=0\)(đk: \(x\ge0\))
\(\Leftrightarrow\left(\sqrt{x}-1\right)\left(\sqrt{x}-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=1\\\sqrt{x}=4\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=16\end{matrix}\right.\) (tm)
Vậy...
27 tháng 5 2021
1) Bạn tự làm
2) ĐK: \(x\ge3\)
PT \(\Leftrightarrow\sqrt{x-3}\left(1-2\sqrt{x}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-3}=0\\2\sqrt{x}=1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{4}\left(loại\right)\end{matrix}\right.\)
Vậy ...
3) ĐK: \(x>-\dfrac{5}{7}\)
PT \(\Rightarrow9x-7=7x+5\) \(\Leftrightarrow x=6\)
Vậy ...
4) ĐK: \(x\ge0\)
PT \(\Leftrightarrow x-4\sqrt{x}-\sqrt{x}+4=0\)
\(\Leftrightarrow\left(\sqrt{x}-4\right)\left(\sqrt{x}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=4\\\sqrt{x}=1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=16\\x=1\end{matrix}\right.\)
Vậy ...
AH
Akai Haruma
Giáo viên
4 tháng 9 2021
1. ĐKXĐ: $x\geq 4$
PT $\Leftrightarrow \sqrt{x-1}=5-\sqrt{x-4}$
$\Rightarrow x-1=25+x-4-10\sqrt{x-4}$
$\Leftrightarrow 22=10\sqrt{x-4}$
$\Leftrightarrow 2,2=\sqrt{x-4}$
$\Leftrightarrow 4,84=x-4\Leftrightarrow x=8,84$
(thỏa mãn)
2. ĐKXĐ: $x\geq 0$
PT $\Leftrightarrow (2x-2\sqrt{x})-(5\sqrt{x}-5)=0$
$\Leftrightarrow 2\sqrt{x}(\sqrt{x}-1)-5(\sqrt{x}-1)=0$
$\Leftrightarrow (\sqrt{x}-1)(2\sqrt{x}-5)=0$
$\Leftrightarrow \sqrt{x}-1=0$ hoặc $2\sqrt{x}-5=0$
$\Leftrightarrow x=1$ hoặc $x=\frac{25}{4}$ (tm)
AH
Akai Haruma
Giáo viên
4 tháng 9 2021
3. ĐKXĐ: $x\geq 3$
Bình phương 2 vế thu được:
$3x-2+2\sqrt{(2x+1)(x-3)}=4x$
$\Leftrightarrow 2\sqrt{(2x+1)(x-3)}=x+2$
$\Leftrightarrow 4(2x+1)(x-3)=(x+2)^2$
$\Leftrightarrow 4(2x^2-5x-3)=x^2+4x+4$
$\Leftrightarrow 7x^2-24x-16=0$
$\Leftrightarrow (x-4)(7x+4)=0$
Do $x\geq 3$ nên $x=4$
Thử lại thấy thỏa mãn
Vậy $x=4$
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 7 2021
1.
ĐKXĐ: \(x\ge3\)
Đặt \(\sqrt{x-3}=t\ge0\Rightarrow x=t^2+3\)
Pt trở thành:
\(t^2+3-7t-9=0\)
\(\Leftrightarrow t^2-7t-6=0\)
\(\Rightarrow\left[{}\begin{matrix}t=\dfrac{7-\sqrt{73}}{2}< 0\left(loại\right)\\t=\dfrac{7+\sqrt{73}}{2}\end{matrix}\right.\)
\(\Rightarrow\sqrt{x-3}=\dfrac{7+\sqrt{73}}{2}\)
\(\Rightarrow x=\dfrac{67+7\sqrt{73}}{2}\)
Nghiệm xấu quá, em nói giáo viên ra đề kiểm tra lại đề là \(x-7\sqrt{x-3}-9=0\) hay \(x-7\sqrt{x-3}+9=0\) nhé
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 7 2021
2.
ĐKXĐ: \(x\ge2\)
\(\sqrt{x+3}+\sqrt{x-2}=5\)
\(\Leftrightarrow2x+1+2\sqrt{\left(x+3\right)\left(x-2\right)}=25\)
\(\Leftrightarrow\sqrt{x^2+x-6}=12-x\) (\(x\le12\))
\(\Rightarrow x^2+x-6=\left(12-x\right)^2\)
\(\Leftrightarrow x^2+x-6=144-24x+x^2\)
\(\Rightarrow x=6\)
Cách 2:
\(\Leftrightarrow\sqrt{x+3}-3+\sqrt{x-2}-2=0\)
\(\Leftrightarrow\dfrac{x-6}{\sqrt{x+3}+3}+\dfrac{x-6}{\sqrt{x-2}+2}=0\)
\(\Leftrightarrow\left(x-6\right)\left(\dfrac{1}{\sqrt{x+3}+3}+\dfrac{1}{\sqrt{x-2}+2}\right)=0\)
\(\Leftrightarrow x=6\)
AH
Akai Haruma
Giáo viên
14 tháng 7 2021
2. ĐKXĐ: $x\geq 2$
PT \(\Rightarrow x+3=(5-\sqrt{x-2})^2\)
\(\Leftrightarrow x+3=25+x-2-10\sqrt{x-2}\)
\(\Leftrightarrow 20=10\sqrt{x-2}\Leftrightarrow x-2=4\Leftrightarrow x=6\)
Thử lại thấy thỏa mãn
Vậy $x=6$
AH
Akai Haruma
Giáo viên
14 tháng 7 2021
3. ĐKXĐ: $x\geq -4$
PT $\Leftrightarrow \sqrt{(x+4)-4\sqrt{x+4}+4}=3$
$\Leftrightarrow \sqrt{(\sqrt{x+4}-2)^2}=3$
$\Leftrightarrow |\sqrt{x+4}-2|=3$
$\Leftrightarrow \sqrt{x+4}-2=\pm 3$. TH $\sqrt{x+4}-2=-3$ loại vì $\sqrt{x+4}-2\geq -2> -3$
Do đó: $\sqrt{x+4}-2=3$
$\Leftrightarrow \sqrt{x+4}=5$
$\Leftrightarrow x+4=25$
$\Leftrightarrow x=21$ (thỏa mãn)
Vậy $x=21$
2 tháng 9 2021
a,ĐK: x≥4
Ta có: \(2\sqrt{x-4}-\dfrac{1}{3}\sqrt{9x-36}=4-\sqrt{x-4}\)
\(\Leftrightarrow2\sqrt{x-4}-\sqrt{x-4}=4-\sqrt{x-4}\)
\(\Leftrightarrow2\sqrt{x-4}=4\)
\(\Leftrightarrow\sqrt{x-4}=2\Leftrightarrow x-4=4\Leftrightarrow x=8\left(tm\right)\)
2 tháng 9 2021
b, ĐK: x≥2
Ta có: \(3\sqrt{x-2}-\sqrt{x^2-4}=0\)
\(\Leftrightarrow3\sqrt{x-2}-\sqrt{\left(x-2\right)\left(x+2\right)}=0\)
\(\Leftrightarrow\sqrt{x-2}\left(3-\sqrt{x+2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-2}=0\\3-\sqrt{x+2}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-2=0\\\sqrt{x+2}=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x+2=9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=7\end{matrix}\right.\)
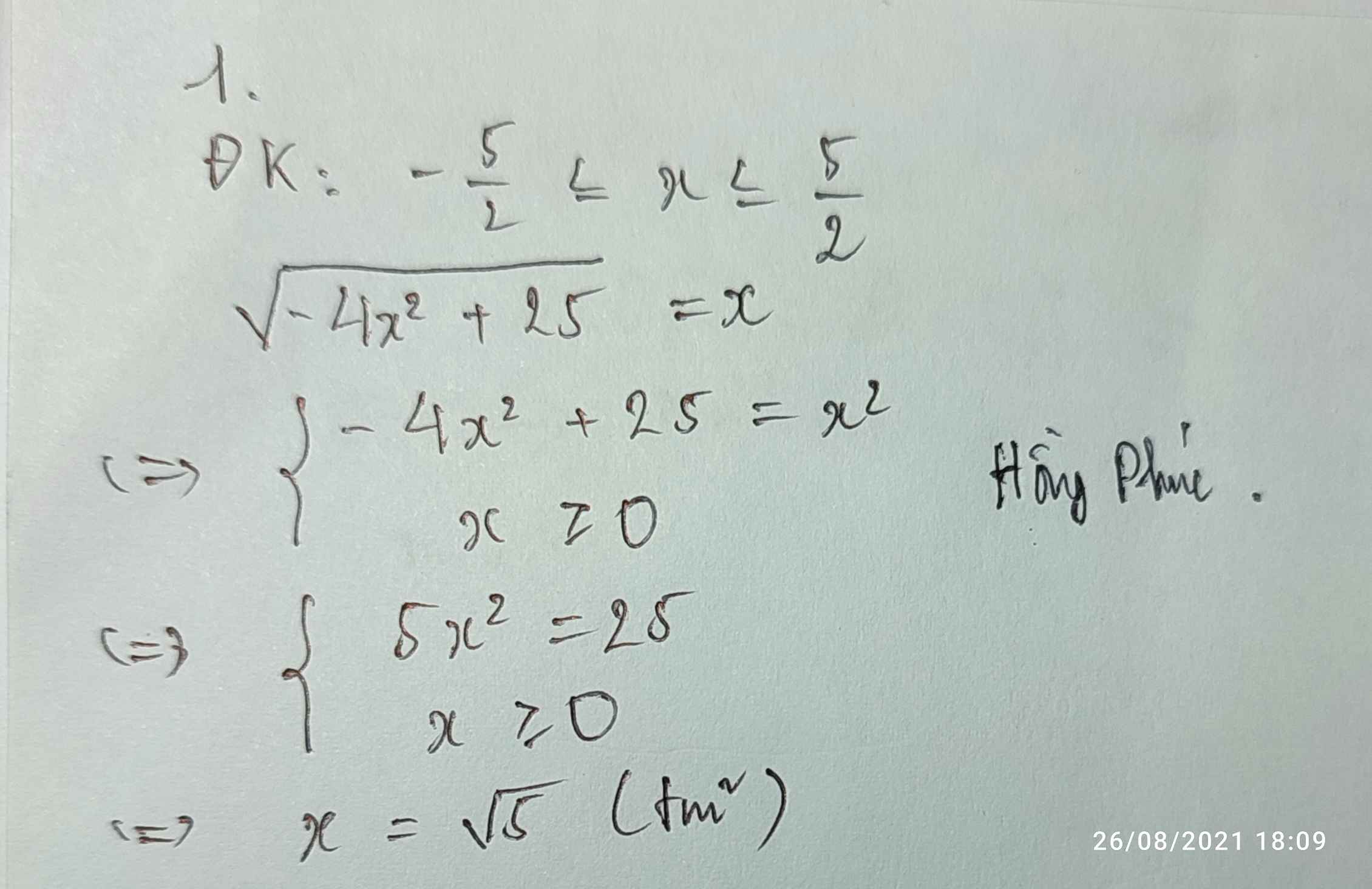
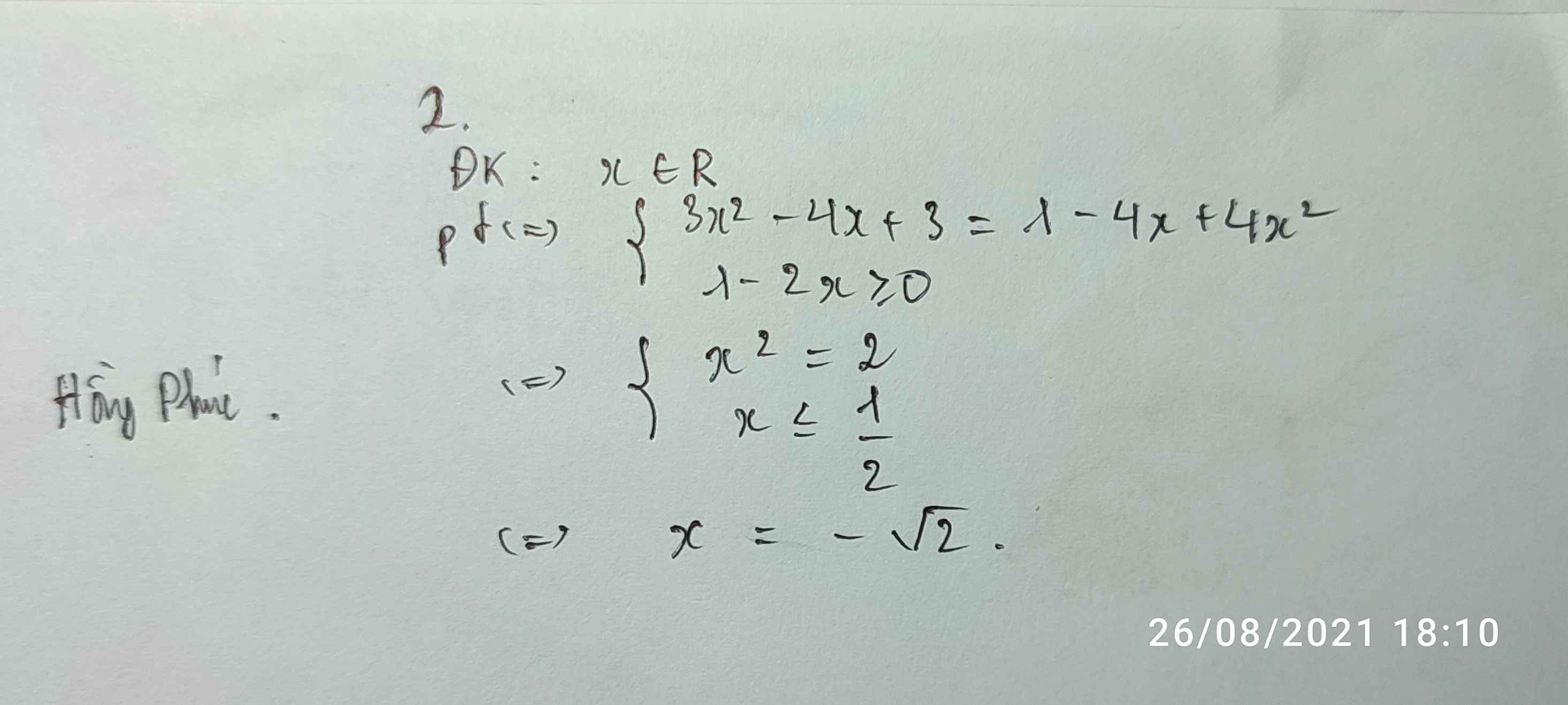
2\(\sqrt{3}\) - \(\sqrt{4+x^2}\) = 0 vì 4 + \(x^2\) ≥ 0 ∀ \(x\) vậy \(\sqrt{4+x^2}\) có nghĩa với ∀\(x\)
2\(\sqrt{3}\) - \(\sqrt{4+x^2}\) = 0
\(\sqrt{4+x^2}\) = 2\(\sqrt{3}\)
4 + \(x^2\) = 12
\(x^2\) = 12 - 4
\(x^2\) = 8
\(\left[{}\begin{matrix}x=-\sqrt{8}\\x=\sqrt{8}\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-2\sqrt{2}\\x=2\sqrt{2}\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-2\sqrt{2}\\x=2\sqrt{2}\end{matrix}\right.\)