K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
O
26 tháng 7 2019
a) Ta có 290>289
<=> \(\sqrt{290}\) > \(\sqrt{289}\)
<=> \(\sqrt{290}\) > 17
Vậy ..........
JK
26 tháng 7 2019
\(a,290>289\)
\(\Rightarrow\sqrt{290}>\sqrt{289}\)
\(\Rightarrow\sqrt{290}>17\)
\(b,\sqrt{7}+\sqrt{15}< \sqrt{9}+\sqrt{16}\)
\(\Rightarrow\sqrt{7}+\sqrt{15}< 3+4\)
\(\Rightarrow\sqrt{7}+\sqrt{15}< 7\)
VN
Võ Ngọc Phương
VIP
24 tháng 10 2023
Ta có:
\(\left(-16\right)^{11}=\left(-2^4\right)^{11}=\left(-2\right)^{4.11}=\left(-2\right)^{44}\)
\(\left(-32\right)^9=\left(-2^5\right)^9=\left(-2\right)^{5.9}=\left(-2\right)^{45}\)
Vì \(44< 45\) nên \(\left(-2\right)^{44}>\left(-2\right)^{45}\)
Vậy \(\left(-16\right)^{11}>\left(-32\right)^9\)
NT
3
AH
Akai Haruma
Giáo viên
25 tháng 7 2023
Lời giải:
$\sqrt{17}+\sqrt{10}> \sqrt{16}+\sqrt{9}=4+3=7$
ND
Nguyễn Đức Trí
VIP
25 tháng 7 2023
\(\sqrt[]{17}+\sqrt[]{10}\Rightarrow\left(\sqrt[]{17}+\sqrt[]{10}\right)^2=17+10+2\sqrt[]{70}=27+2\sqrt[]{70}< 27+2\sqrt[]{100}=47\)
mà \(7^2=49>47\)
\(\Rightarrow\sqrt[]{17}+\sqrt[]{10}< 7\)
3 tháng 7 2023
`@` `\text {Ans}`
`\downarrow`
Ta có:
\(5^{333}=\left(5^3\right)^{111}=125^{111}\)
\(11^{222}=\left(11^2\right)^{111}=121^{111}\)
Vì `125 > 121 =>`\(125^{111}>121^{111}\)
`=>`\(5^{333}>11^{222}\)
Vậy, \(5^{333}>11^{222}\)
_____
`@` So sánh lũy thừa cùng cơ số:
Nếu `m > n =>`\(a^m>a^n\left(m,n\ne0,a>1\right)\)
`@` So sánh lũy thừa cùng số mũ:
Nếu `a > b =>`\(a^m>b^m\left(a,b>1,m\ne0\right)\)
`@` `\text {Kaizuu lv uuu}`
26 tháng 6 2023
`@` `\text {Ans}`
`\downarrow`
`a)`
\(3^{200}\text{ và }2^{300}\)
\(3^{200}=\left(3^2\right)^{100}=9^{100}\)
\(2^{300}=\left(2^3\right)^{100}=8^{100}\)
Vì `9 > 8 => 9^100 > 8^100`
`=> 3^200 > 2^300`
`b)`
\(27^{101}\text{ và }81^{35}\)
\(27^{101}=\left(3^3\right)^{101}=3^{303}\)
\(81^{35}=\left(3^4\right)^{35}=3^{140}\)
Vì `303 > 140 => 3^303 > 3^140`
`=> 27^101 > 81^35`
`c)`
\(2^{332}\text{ và }3^{223}\)
\(2^{332}< 2^{333}=\left(2^3\right)^{111}=8^{111}\)
\(3^{223}>3^{222}=\left(3^2\right)^{111}=9^{111}\)
Vì `9 > 8 => 9^111 > 8^111`
`=> 2^332 < 3^223.`
26 tháng 6 2023
a: 3^200=9^100
2^300=8^100
mà 9>8
nên 3^200>2^300
b: 27^101=3^303
81^35=3^140
mà 303>140
nên 27^101>81^35
c: 2^332<2^333=8^111
3^223>3^222=9^111
mà 9>8
nên 3^223>8^111>2^332
ND
Nguyễn Đức Trí
VIP
9 tháng 9 2023
a) \(\dfrac{35}{101}=\dfrac{105}{303}< \dfrac{189}{303}\Rightarrow\dfrac{35}{101}< \dfrac{189}{303}\)
b) \(\dfrac{11}{13}< \dfrac{11+2}{13+2}=\dfrac{13}{15}< \dfrac{14}{15}\Rightarrow\dfrac{11}{-13}>\dfrac{-14}{15}\)
c) \(-\dfrac{32}{19}< 0< \dfrac{23}{32}\Rightarrow-\dfrac{32}{19}< \dfrac{23}{32}\)
d) \(1,561< 1,5661\Rightarrow-1,561>-1,5661\)
e) \(0,1=\dfrac{1}{10}=\dfrac{40}{400}< \dfrac{40+56}{400+56}=\dfrac{96}{456}< \dfrac{176}{456}\Rightarrow0,1< \dfrac{176}{456}\)
g) \(0,3=\dfrac{3}{10}=\dfrac{9}{30}< \dfrac{9+8}{30+8}=\dfrac{17}{38}< \dfrac{19}{38}\Rightarrow0,3< \dfrac{19}{38}\Rightarrow-0,3>\dfrac{-19}{38}\)
PL
3
TQ
3
23 tháng 2 2022
\(2^{333}=\left(2^3\right)^{111}=8^{111}\\ 3^{222}=\left(3^2\right)^{111}=9^{111}\)
VÌ\(8^{111}< 9^{111}\Rightarrow2^{333}< 3^{222}\)
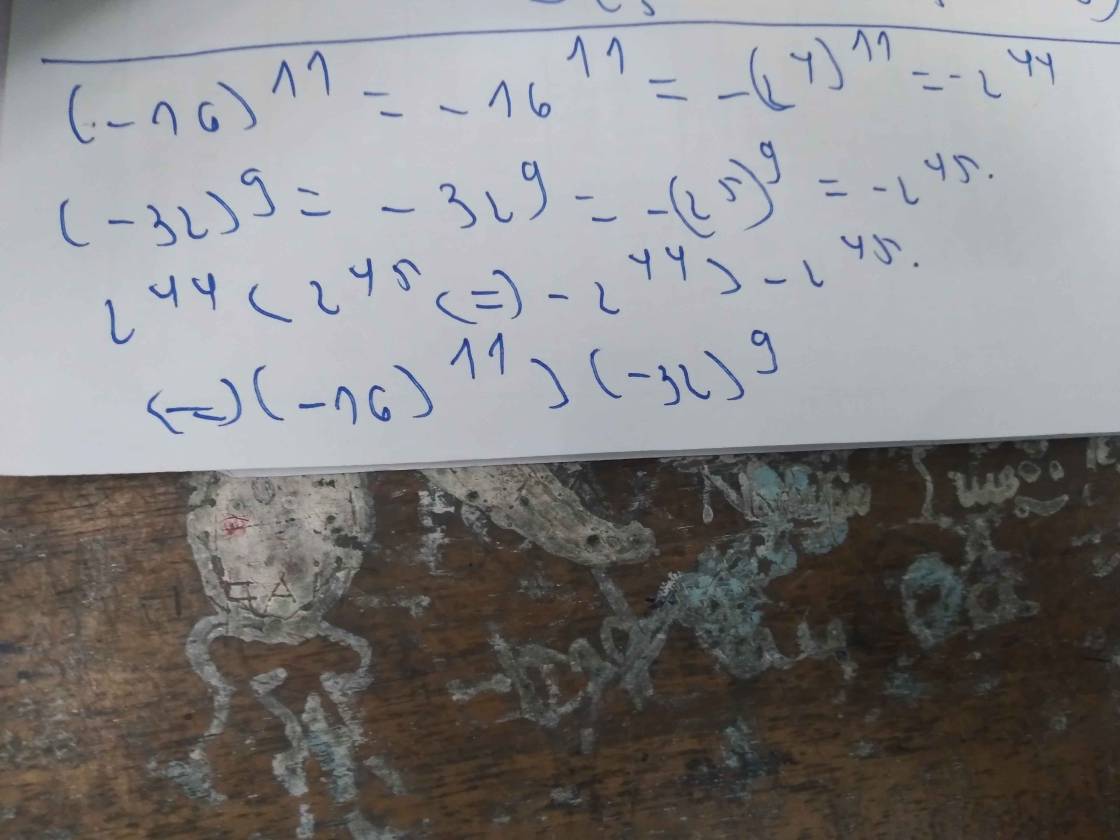
a) ta có: 290 = (25)18 = 3218
536 = (52)18 = 2518
=> ...
b) 227 = (23)9 = 89
318 = (32)9 = 99
=>...