Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=\dfrac{2024^{2023}+1}{2024^{2024}+1}\)
\(2024A=\dfrac{2024^{2024}+2024}{2024^{2024}+1}=\dfrac{\left(2024^{2024}+1\right)+2023}{2024^{2024}+1}=\dfrac{2024^{2024}+1}{2024^{2024}+1}+\dfrac{2023}{2024^{2024}+1}=1+\dfrac{2023}{2024^{2024}+1}\)
\(B=\dfrac{2024^{2022}+1}{2024^{2023}+1}\)
\(2024B=\dfrac{2024^{2023}+2024}{2024^{2023}+1}=\dfrac{\left(2024^{2023}+1\right)+2023}{2024^{2023}+1}=\dfrac{2024^{2023}+1}{2024^{2023}+1}+\dfrac{2023}{2024^{2023}+1}=1+\dfrac{2023}{2024^{2023}+1}\)
Vì \(2024>2023=>2024^{2024}>2024^{2023}\)
\(=>2024^{2024}+1>2024^{2023}+1\)
\(=>\dfrac{2023}{2024^{2023}+1}>\dfrac{2023}{2024^{2024}+1}\)
\(=>A< B\)
\(#PaooNqoccc\)

a) \(2023^{2024}\) và \(2023^{2023}\)
vì 2024 > 2023 nên 20232024 > 20232023
Vậy 20232024 > 20232023
b) \(17^{2024}\) và \(18^{2024}\)
vì 17 < 18 nên 172024 < 18 2024
Vậy 172024 < 182024

Lời giải:
Ta có:
$(x+y+z)(\frac{1}{x}+\frac{1}{y}+\frac{1}{z})=2023.\frac{2024}{2023}$
$\Leftrightarrow 1+\frac{x}{y}+\frac{x}{z}+\frac{y}{x}+1+\frac{y}{z}+\frac{z}{x}+\frac{z}{y}+1=2024$
$\Leftrightarrow 3+\frac{x+z}{y}+\frac{y+z}{x}+\frac{x+y}{z}=2024$
$\Leftrightarrow 3+B=2024$
$\Leftrightarrow B=2021$

A=2x^2+9y^2-6xy-6x-12y+2024
A = (x^2 -6xy +9y^2) + 4(x -3y) + x^2 - 10x + 2024
A = (x -3y)^2 +4(x -3y) + 4 + x^2 -10x +25 + 1995
A = (x -3y +2)^2 + (x -5)^2 + 1995 \geq 1995
Min A = 1995
x - 5 = 0 => x = 5
Và x - 3y + 2 = 0 hay 5 -3y +2 = 0 => -3y = -7 => y = 7/3
\(K\)\(nha!~!\)

\(A=x^2-2x+2024\)
\(A=x^2-2x+1+2023=\left(x-1\right)^2+2023\ge2023\)
Min A = 2023 khi x = 1

=x^2-2x+1+2023
=(x-1)^2+2023>=2023
Dấu = xảy ra khi x=1
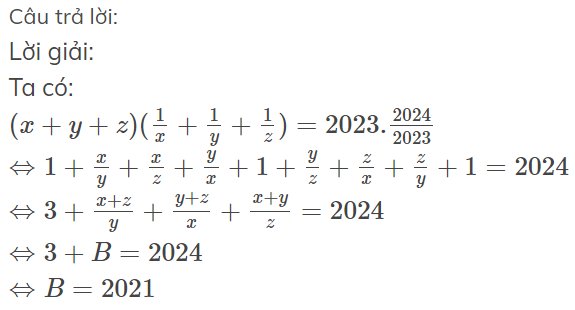
\(A=\dfrac{2024}{1.2}+\dfrac{2024}{2.3}+\dfrac{2024}{3.4}+...+\dfrac{2024}{2023.2024}\)
\(A=2024.\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{2023.2024}\right)\)
\(A=2024.\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2023}-\dfrac{1}{2024}\right)\)
\(A=2024.\left(1-\dfrac{1}{2024}\right)\)
\(A=2024.\dfrac{2023}{2024}\)
\(A=\dfrac{2024}{1}.\dfrac{2023}{2024}\)
\(A=1.2023\)
\(A=2023\)
\(\Rightarrow\) Vậy \(A=2023\)