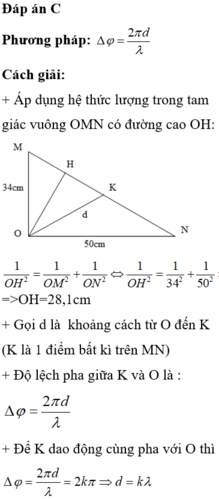
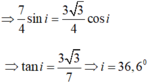Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp: Định luật khúc xạ ánh sáng n1sini = n2sinr
Cách giải:
Ta có:
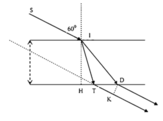
![]()
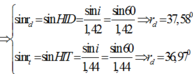
![]()
![]()
Từ hình v có:![]()
=> Bề rộng dải quang phổ liên tục khi chùm sáng ló ra khỏi tấm nhựa:
DK = TD.sinDTK = 0,168.sin30 = 0,084cm

Đáp án B
Phương pháp: Phương trình giao thoa sóng trong giao thoa sóng hai nguồn cùng pha:
u M = 2 acos π ( d 2 - d 1 ) λ cos [ ωt - π ( d 2 + d 1 ) λ ]
Cách giải:
Bước sóng: λ = 2cm
Phương trình sóng tại M:
u M = 2 acos π ( MA - MB ) λ cos [ ωt - π ( MA + MB ) λ ]
X là điểm dao động với biên độ cực đại và ngược pha với M.
Phương trình sóng tại X:
u X = 2 acos π ( XA - XB ) λ cos [ ωt - π ( XA + XB ) λ ]
Vì X và M thuộc elip => M + MB = X + XB
=> uM và uX chỉ khác nhau về:
cos π ( MA - MB ) λ ; cos π ( XA - XB ) λ
Vì M thuộc trung trực của AB
⇒ cos π ( MA - MB ) λ = 1
X ngược pha với M
⇔ cos π ( XA - XB ) λ = - 1 ⇔ X A - X B = ( 2 k + 1 ) λ
- AB ≤ ( 2 k + 1 ) λ ≤ AB ⇔ - 19 ≤ ( 2 k + 1 ) λ ≤ 19 ⇒ - 5 , 25 ≤ k ≤ 4 , 25
=> Có 10 điểm dao động với biên độ cực đại và ngược pha với M trên đoạn B
=> Trên elip có 20 điểm dao động với biên độ cực đại và ngược pha với M.

Đáp án C
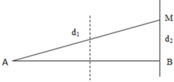
+ Bước sóng: λ = v/f = 0,6/40 = 1,5cm
+ Số cực đại giao thoa trên đoạn thẳng nối hai nguồn bằng số giá trị k nguyên thoả mãn:
- A B λ < k < A B λ ⇔ - 10 1 , 5 < k < 10 1 , 5 ⇔ - 6 , 67 < k < 6 , 67 ⇒ k = 0 ; ± 1 , ± 2 , . . . . , ± 6
+ Ta có: S A M B = 1 2 A B . M B ⇒ ( S A M B ) m i n ⇔ ( M B ) m i n ⇔ M thuộc cực đại ứng với kmax => d1 – d2 = 6λ = 9cm.
+ Áp dụng định lí Pi – ta – go trong tam giác vuông AMB có:
A B 2 + d 2 2 = d 1 2 ⇔ 10 2 + d 2 2 = ( d 2 + 9 ) 2 ⇒ d 2 = 19 18 c m = M B ⇒ S A M B = 1 2 A B . M B = 1 2 . 10 . 19 18 = 5 , 28 c m 2