Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét cả hai trường hợp sau:
a) Xét trường hợp điểm M nằm giữa hai điểm A và N; Điểm N nằm giữa hai điểm B và M.
- Vì M nằm giữa A và M nên AN= AM+MN (1)
- Vi N nằm giữa B và M nên BM= BN + MN (2)
Mà AN= BM (đề bài) nên từ (1) và (2) suy ra AM + MN = BN + MN
Do đó: AM = BN.
b) Xét trường hợp điểm N nằm giữa A và M; điẻm M nằm giữa B và N.
- Vì N nằm giữa A và M nên AN + NM= AM (3)
- Vì M nằm giữa B và N nên BM + MN= BN(4)
Mà AN=BM(Đề bài) nên từ (3) và(4) AM=BN

TH1: AN < AB /2
+) M nằm giữa A và B nên AM + MB = AB => AM = AB - BM
+) N nằm giữa A và B nên AN + NB = AB => BN = AB - AN
mà BM = AN nên AB - BM = AB - AN => AM = BN
TH2: Nếu AN > AB/2
+) M nằm giữa A và B nên AM + MB = AB => AM = AB - BM
+) N nằm giữa A và B nên AN + NB = AB => BN = AB - AN
mà BM = AN nên AB - BM = AB - AN => AM = BN
Chú ý: Bài này xét 2 trường hợp vẫn đúng nhưng không cần thiết phải làm cả 2 trường hợp. Chỉ cần làm 1 truơngf hợp mà không ảnh hường gì
Lời giải:
Chúng ta sẽ giải bài toán theo hai trường hợp như trong hình:
Trường hợp a)
Vì M nằm giữa hai điểm A và N nên AN = AM + MN
Vì N nằm giữa hai điểm B và M nên BM = BN + MN
Theo đề bài: AN = BM nên AM + MN = BN + MN => AM = BN
(áp dụng tính chất: a + b = c + b => a = c)
Trường hợp b)
Vì N nằm giữa hai điểm A và M nên AN + MN = AM => AN = AM - MN
Vì M nằm giữa hai điểm B và N nên BM + MN = BN => BM = BN - MN
Theo đề bài: AN = BM nên AM - MN = BN - MN => AM = BN
(áp dụng tính chất: a - b = c - b => a = c)
Tóm lại: trong cả hai trường hợp thì hai đoạn thẳng AM và BN có độ dài bằng nhau.

Chúng ta sẽ giải bài toán theo hai trường hợp như trong hình:
Trường hợp a)
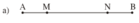
Vì M nằm giữa hai điểm A và N nên AN = AM + MN
Vì N nằm giữa hai điểm B và M nên BM = BN + MN
Theo đề bài: AN = BM nên AM + MN = BN + MN ⇒ AM = BN
(áp dụng tính chất: a + b = c + b ⇒ a = c)
Trường hợp b)

Vì N nằm giữa hai điểm A và M nên AN + MN = AM ⇒ AN = AM - MN
Vì M nằm giữa hai điểm B và N nên BM + MN = BN ⇒ BM = BN - MN
Theo đề bài: AN = BM nên AN - MN = BN - MN ⇒ AM = BN
(áp dụng tính chất: a - b = c - b ⇒ a = c)
Tóm lại: trong cả hai trường hợp thì hai đoạn thẳng AM và BN có độ dài bằng nhau

Trường hợp (hình a)
Ta có: Điểm M nằm giữa A và N
=> AM + MN = AN
Mà: Điểm N nằm giữa M và B
=> MN + NB = MB
Mà AN = MB
Vậy AM + MN = MN + NB
=> AM = BN
Trường hợp (hình b)
Ta có: Điểm N nằm giữa A và M
=> AN + NM = AM
Mà: Điểm M nằm giữa N và B
=> NM + MB = NB
Mà: AM = NB
=> AN + NM = NM + MB
Vậy AM = BN




