Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

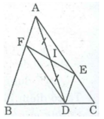
Ta có: DE //AB (gt) hay DE //AF
Và DF //AC (gt) hay DF //AE
Suy ra, tứ giác AEDF là hình bình hành.
Lại có, I là trung điểm của AD nên I cũng là trung điểm EF (tính chất hình bình hành)
Vậy E và F đối xứng qua tâm I.

Bài 1:

Tứ giác ABCD là hình bình hành:
⇒ AB // CD hay BM // CD
Xét tứ giác BMCD ta có:
BM // CD
BM = CD( = AB ) (gt)
Suy ra: Tứ giác BMCD là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ MC // BD và MC = BD (1)
+) Ta có AD // BC (gt) haỵ DN // BC
Xét tứ giác BCND ta có: DN // BC và DN = BC (vì cùng bằng AD)
Suy ra: Tứ giác BCND là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
⇒ CN // BD và CN = BD (2)
Từ (1) và (2) theo tiên đề Ơ- clit suy ra: M, C, N thẳng hàng và MC = CN( = BD).
Bài 2:

Ta có: DE //AB (gt) hay DE //AF
Và DF //AC (gt) hay DF //AE
Suy ra, tứ giác AEDF là hình bình hành.
Lại có, I là trung điểm của AD nên I cũng là trung điểm EF (tính chất hình bình hành)
Vậy E và F đối xứng qua tâm I.

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
b: Xét ΔABC có
D là trung điểm của BC
DE//AC
Do đó: E là trung điểm của AB
Xét tứ giác AIBD có
E là trung điểm của AB
E là trung điểm của ID
Do đó: AIBD là hình bình hành
mà AB\(\perp\)DI
nên AIBD là hình thoi

Ta có: EF // BD (gt)
BF // ED (gt)
Suy ra EF = BD; BF = DE (t/c đoạn chắn)
Trên AB lấy K sao cho AF = BK
ΔAFEΔAFE và ΔKBDΔKBD có:
AF = BK (cách vẽ)
AFE = KBD (đồng vị)
EF = BD (cmt)
Do đó, ΔAFE=ΔKBD(c.g.c)ΔAFE=ΔKBD(c.g.c)
=> AE = KD (2 cạnh t/ứ)
= BF = ED (theo gt AE = BF, theo cmt BF = ED)
Kẻ DM⊥AB;DN⊥ACDM⊥AB;DN⊥AC
ΔΔ DMK vuông tại M và ΔΔ DNE vuông tại N có:
DK = DE (cmt)
MKD = NED (cùng đồng vị với FAE)
Do đó, ΔDMK=ΔDNEΔDMK=ΔDNE (cạnh huyền - góc nhọn)
=> DM = DN (2 cạnh t/ứ)
=> D cách đều AB và AC (đpcm)
thông cảm nha mk llafm vội nên ko để ý nên ko chác chắn bài

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật

a) Theo gt ta có :
FD // AC => FD // AE ( E \(\in AC\)) ( 1)
DE // AB => DE // AF ( F \(\in AB\) ) (2)
từ (1)(2) \(\Rightarrow AEDF\) là hình bình hành ( theo dấu hiệu nhận biết hình bình 1)
b)
theo a) tao có AEDF là hình bình hành
hình bình hành có 2 đường chéo AD và EF giao nhau tại I
=> I là trung điểm của 2 đường chéo AD và EF ( t/c hình bình hành )
=> \(IF=IE\) hay F đối xứng với E qua I
a)Xét tứ giác AEDF có: DE//AB, DF//AC
\(\Rightarrow\)AEDE là hình bình hành
b) Vì 2 đường chéo của hình bình hành cắt nhau tại trung điểm mỗi đường nên IA=ID, IF=IE suy ra E đối xứng với F qua I
Hình đâu?