Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Áp dụng Cauchy Schwars ta có:
\(M=\frac{a^2}{a+1}+\frac{b^2}{b+1}+\frac{c^2}{c+1}\ge\frac{\left(a+b+c\right)^2}{a+b+c+3}=\frac{9}{6}=\frac{3}{2}\)
Dấu "=" xảy ra khi: a = b = c = 1
b) \(N=\frac{1}{a}+\frac{4}{b+1}+\frac{9}{c+2}\ge\frac{\left(1+2+3\right)^2}{a+b+c+3}=\frac{36}{6}=6\)
Dấu "=" xảy ra khi: x=y=1

Ta chứng minh BĐT sau:
\(\dfrac{1}{x^3+x+2}\ge\dfrac{-x^2+3}{8}\) với \(x>0\)
Thật vậy, BĐT tương đương:
\(\left(x^2-3\right)\left(x^3+x+2\right)+8\ge0\)
\(\Leftrightarrow\left(x-1\right)^2\left(x^3+2x^2+x+2\right)\ge0\) (luôn đúng)
Áp dụng:
\(\Rightarrow VT\ge\dfrac{-a^2+3}{8}+\dfrac{-b^2+3}{8}+\dfrac{-c^2+3}{8}=\dfrac{9-\left(a^2+b^2+c^2\right)}{8}=\dfrac{3}{4}\)
Dấu "=" xảy ra khi \(a=b=c=1\)

Rất khủng khiếp (tại cái chương trình của em nó xấu:v) nhưng nó là một cách chứng minh:
\(\Leftrightarrow\left(\frac{a}{b}+\frac{b}{c}+\frac{c}{a}\right)^2\ge\frac{27\left(a^2+b^2+c^2\right)}{\left(a+b+c\right)^2}\)
\(\Leftrightarrow\left(\frac{x}{y}+\frac{y}{z}+\frac{z}{x}\right)^2\ge\frac{27\left(x^2+y^2+z^2\right)}{\left(x+y+z\right)^2}\)
Sau khi quy đồng, ta cần chứng minh biểu thức sau đây không âm:

Hiển nhiên đúng vì \(x=min\left\{x,y,z\right\}\)
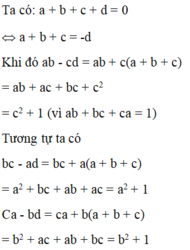

a) Co:a+b+c+d=0
=> a+b=-(c+d)
=> (a+b)^3=-(c+d)^3
=> a^3+b^3+3ab(a+b)=-c^3-d^3-3cd(c+d)
=> a^3+b^3+c^3+d^3=-3ab(a+b)-3cd(c+d)
=> a^3+b^3+c^3+d^3=3ab(c+d)-3cd(c+d) ( vi a+b = - (c+d))
==> a^3 +b^^3+c^3+d^3==3(c+d)(ab-cd) (dpcm)
b) Co: a+b+c=9
=> (a+b+c)^2 = 49
=> a^2 + b^2 +c^2 + 2(ab + bc + ca) = 49
=> 2(ab+bc+ca) = -4
=> ab+bc+ca= -2
2) \(8x^3-12x^2+6x-1=0\leftrightarrow\left(2x-1\right)^3=0\leftrightarrow2x-1=0\leftrightarrow x=\frac{1}{2}\)