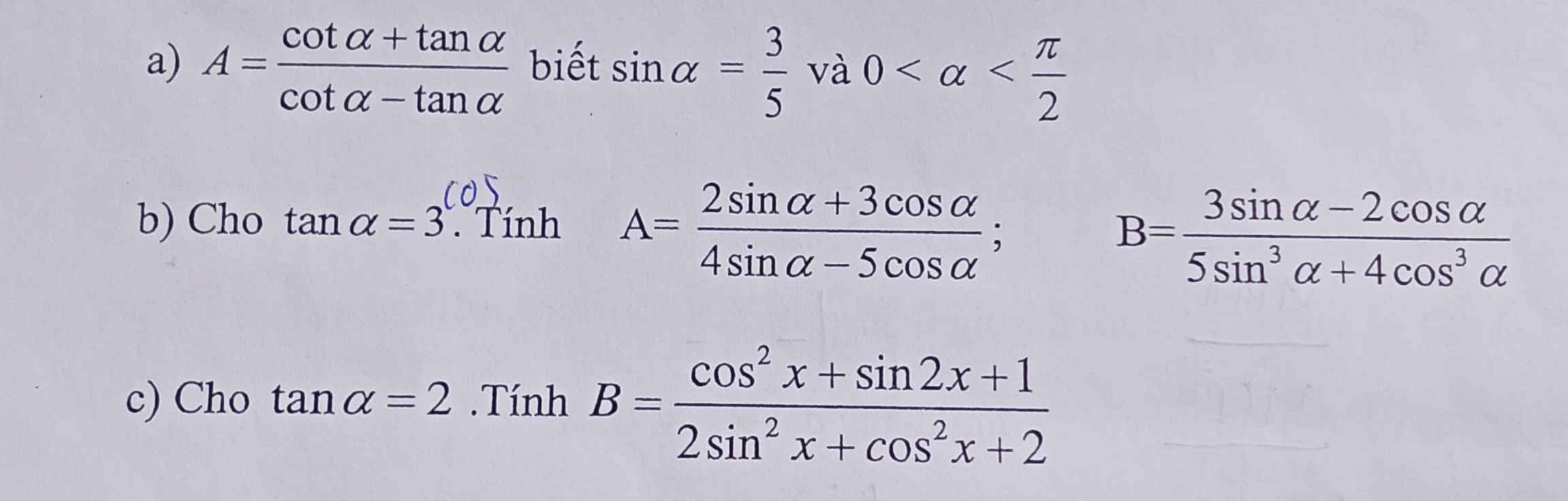CT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2020
\(\Leftrightarrow2\left|x-1\right|\le3x-6\)
- Với \(x< 2\Rightarrow3x-6< 0\Rightarrow\left\{{}\begin{matrix}VT\ge0\\VP< 0\end{matrix}\right.\) BPT vô nghiệm
- Với \(x\ge2\Rightarrow x-1>0\Rightarrow\left|x-1\right|=x-1\) BPT trở thành:
\(2\left(x-1\right)\le3x-6\Leftrightarrow x\ge4\)
Vậy nghiệm của BPT là \(x\ge4\)
LH
2
28 tháng 9 2016
Ix2-xI+Ix-1I khác 0 .
Nhưng giá trị tuyệt đối luôn lớn hơn 0 . Nên biểu thức trên luôn lớn hơn 0
LT
1
LG
2
20 tháng 9 2020
Ta có \(x^4+x^2+1=\left(x^2+1\right)^2-x^2=\left(x^2+x+1\right)\left(x^2-x+1\right)>0,\forall x\)
Mặt khác: \(x^2-3x+1=2\left(x^2-x+1\right)-\left(x^2+x+1\right)\)
Đặt \(y=\sqrt{\frac{x^2-x+1}{x^2+x+1}}\)(có thể viết điều kiện \(y\ge0\)hoặc chính xác hơn là \(\frac{\sqrt{3}}{3}\le y\le\sqrt{3}\)), ta được:
\(2y^2-1=\frac{-\sqrt{3}}{3}y=0\Leftrightarrow6y^2+\sqrt{3y}-3=0\), ta được \(y=\frac{\sqrt{3}}{3}\)(loại \(y=\frac{-\sqrt{3}}{2}\))
=> Phương trình có nghiệm là x=1
JV
1
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
22 tháng 11 2021
1b)
Song song => (d): x-y +a =0
Vì d đi qua C(2;-2) => 2- (-2)+a=0
<=>a=4
=> d: x-y+4=0
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 4 2022
a.
\(0< a< \dfrac{\pi}{2}\Rightarrow cosa>0\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{4}{5}\)
\(\Rightarrow tana=\dfrac{sina}{cosa}=\dfrac{3}{4}\) ; \(cota=\dfrac{1}{tana}=\dfrac{4}{3}\)
\(\Rightarrow A=\dfrac{\dfrac{4}{3}+\dfrac{3}{4}}{\dfrac{4}{3}-\dfrac{3}{4}}=...\)
b.
\(A=\dfrac{\dfrac{2sina}{cosa}+\dfrac{3cosa}{cosa}}{\dfrac{4sina}{cosa}-\dfrac{5cosa}{cosa}}=\dfrac{2tana+3}{4tana-5}=\dfrac{2.3+3}{4.3-5}=...\)
\(B=\dfrac{\dfrac{3sina}{cos^3a}-\dfrac{2cosa}{cos^3a}}{\dfrac{5sin^3a}{cos^3a}+\dfrac{4cos^3a}{cos^3a}}=\dfrac{3tana\left(1+tan^2a\right)-2\left(1+tan^2a\right)}{5tan^3a+4}=...\) em tự thay số
c.
\(B=\dfrac{cos^2x+2sinx.cosx+1}{sin^2x+3}=\dfrac{\dfrac{cos^2x}{cos^2x}+\dfrac{2sinx.cosx}{cos^2x}+\dfrac{1}{cos^2x}}{\dfrac{sin^2x}{cos^2x}+\dfrac{3}{cos^2x}}\)
\(=\dfrac{1+2tanx+\left(1+tan^2x\right)}{tan^2x+3\left(1+tan^2x\right)}=...\)
NT
1
