K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
DT
4
.
.
.
.
CM
13 tháng 9 2018
Đáp án C
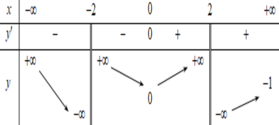
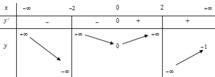
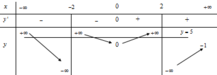
Vì phương trình 
có ba nghiệm phân biệt nên đồ thị hàm số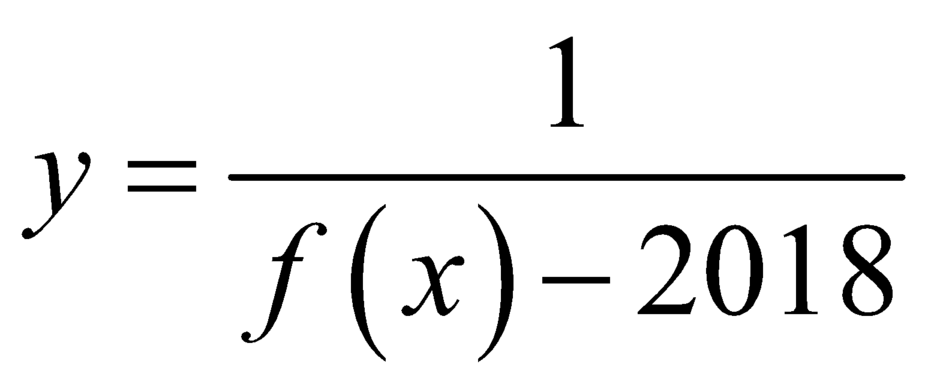 
có ba đường tiệm cận đứng.
Mặt khác, ta có:
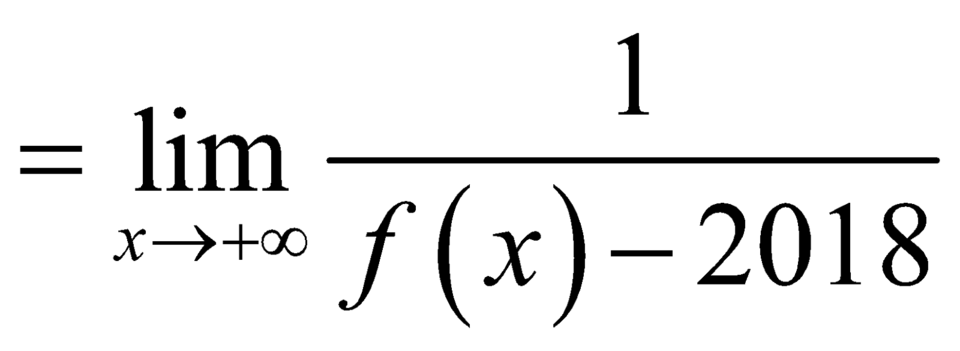
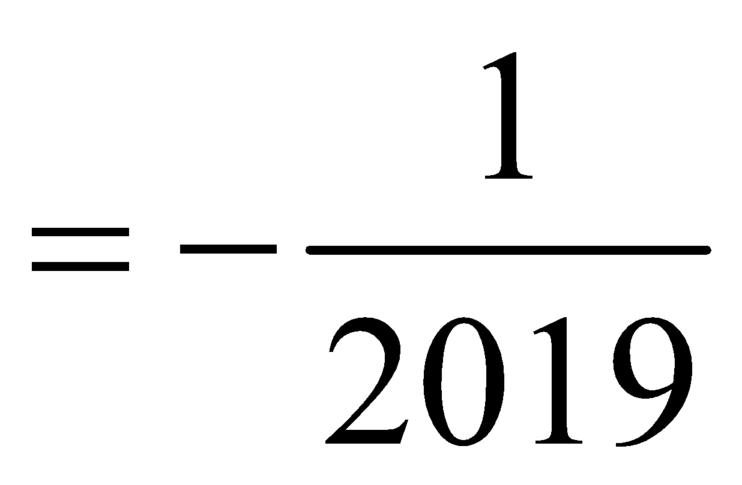nên đường thẳng 
là đường tiệm cận ngang của đồ thị hàm số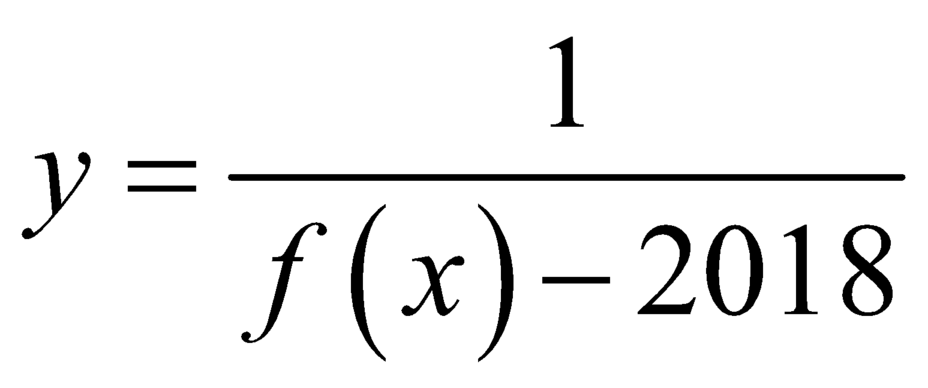 
.
Và 
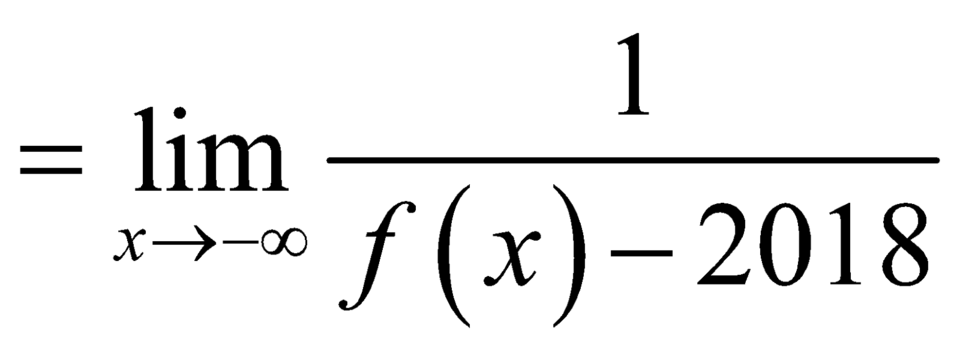
nên đường thẳng y=0 là đường tiệm cận ngang của đồ thị hàm số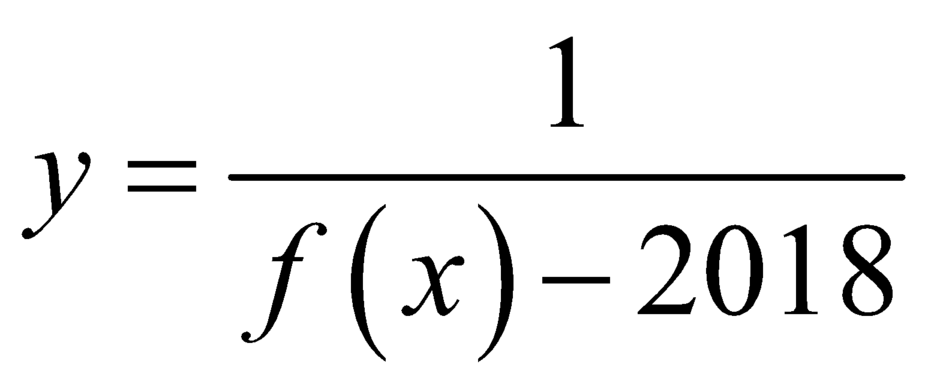 
.
Vậy 
.
BT
7 tháng 12 2017
\(AH=HB=\dfrac{a}{2}\).
\(DH=\sqrt{\left(a\sqrt{3}\right)^2+\left(\dfrac{a}{2}\right)^2}=\dfrac{\sqrt{13}a}{2}\).
\(SH=DH.tan\widehat{SDH}=\dfrac{\sqrt{13}a}{2}.tan60^o=\dfrac{\sqrt{39}a}{2}\).
Thể tích khối chóp S.ABCD là: \(\dfrac{1}{3}.SH.S_{ABCD}=\dfrac{1}{3}.\dfrac{\sqrt{39}a}{2}.a.\sqrt{3}a=\dfrac{\sqrt{13}a^3}{2}\).
QA
0
CM
3 tháng 12 2018
+ Sử dụng tính chất: Hàm số y= logax đồng biến trên TXĐ khi a> 1nên y= f(x) = lnx
là hàm số đồng biến.
+ Sử dụng tính chất: Hàm số y= ax nghịch biến trên R khi 0< a< 1nên
Chọn C
334(L Y)
HỌC TỐT 👍
334.
Học tốt nha!