Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
a) ( a+1)(a+2)(a^2+4)(a-1)(a^2+1)(a-2)
= [(a+1)(a-1)][(a-2)(a+2)](a^2+1)(a^2+4)
=[(a^2+1)(a^2-1)][(a^2+4)(a^2-4)]
=(a^4-1)(a^4-16)
b)(3a+1)^2 + (2-3a)(2+3a)
= 9a2 + 6a +1 + 4 - 9a2
= 6a+5
2.
Ta có a3 +b3 = ( a + b)(a2 -ab + b2) = a2 + 2ab +b2 -3ab = (a+b)2 -3ab = 1-3ab ( dpcm)
1.
a) (a + 1)(a + 2)(a2 + 4)(a - 1)(a2 + 1)(a - 2)
= [(a + 1)(a - 1)][(a + 2)(a - 2)](a2 + 4)(a2 + 1)
= (a2 - 1)(a2 - 4)(a2 + 4)(a2 + 1)
= [(a2 - 1)(a2 + 1)][(a2 - 4)(a2 + 4)]
= (a4 - 1)(a4 - 16)
= a8 - 16a4 - a4 + 16
= a8 - 17a4 + 16
b) (3a + 1)2 + (2 - 3a)(2 + 3a)
= 9a2 + 6a + 1 + 22 - 9a2
= (9a2 - 9a2) + 6a + (1 + 4)
= 6a + 5
2.
a + b = 1
(a + b)3 = 13
a3 + 3a2b + 3ab2 + b3 = 1
a3 + b3 + 3ab(a + b) = 1
a3 + b3 = 1 - 3ab(a + b)
Mà a + b = 1
=> a3 + b3 = 1 - 3ab
Vậy với a + b = 1 thì a3 + b3 = 1 - 3ab

\(N=a^3+b^3+3ab\)
\(=\left(a+b\right)^3-3ab\left(a+b\right)+3ab\)
=1
\(M=\left(a^2+b^2+2-a^2-b^2+2\right)\left[\left(a^2+b^2+2\right)^2+\left(a^2+b^2+2\right)\left(a^2+b^2-2\right)+\left(a^2+b^2-2\right)^2\right]-12\left(a^2+b^2\right)^2\\ M=4\left(a^4+b^4+4+4a^2+4b^2+2a^2b^2+\left(a^2+b^2\right)^2-4+a^4+b^4+4-4a^2-4b^2+2a^2b^2\right)-12\left(a^4+2a^2b^2+b^4\right)\\ M=4\left(3a^4+3b^4+4+6a^2b^2\right)-12\left(a^4+2a^2b^2+b^4\right)\\ M=4\left(3a^4+3b^4+4+6a^2b^2-3a^4-6a^2b^2-3b^4\right)\\ M=4\cdot4=164\)

a) Ta có: \(\dfrac{P}{x+2}=\dfrac{x^2+5x+6}{x^2+4x+4}\)
\(\Leftrightarrow\dfrac{P}{x+2}=\dfrac{\left(x+2\right)\left(x+3\right)}{\left(x+2\right)^2}=\dfrac{x+3}{x+2}\)
hay P=x+3
CMR :1,a2+b2=<a+b>2-2ab
2,a3+b3=<a+b>3-3ab.<a+b>
3,a3-b3=<a-b>3+3ab.<a+b>
Cho :a+b=1
Tính :A=a3+b3+3ab

2
Ta có:
VP=(a+b)3−3ab(a+b)VP=(a+b)3-3ab(a+b)
=a3+b3+3ab(a+b)−3ab(a+b)=a3+b3+3ab(a+b)-3ab(a+b)
=a3+b3=VT(dpcm)
1, \(VT=a^2+b^2=a^2+b^2+2ab-2ab=\left(a+b\right)^2-2ab=VP\left(đpcm\right)\)

\(\left(a+b+c\right)^2=a^2+b^2+c^2\)
=>\(a^2+b^2+c^2+2\left(ab+bc+ac\right)=a^2+b^2+c^2\)
=>\(2\left(ab+bc+ac\right)=0\)
=>ab+bc+ac=0
\(\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}=\dfrac{3}{abc}\)
=>\(\dfrac{\left(bc\right)^3+\left(ac\right)^3+\left(ab\right)^3}{\left(abc\right)^3}=\dfrac{3}{abc}\)
=>\(\left(bc\right)^3+\left(ac\right)^3+\left(ab\right)^3=3\left(abc\right)^2\)
\(\Leftrightarrow\left(ab+bc\right)^3-3\cdot ab\cdot bc\cdot\left(ab+bc\right)+\left(ac\right)^3=3\left(abc\right)^2\)
=>\(\left(-ac\right)^3-3\cdot ab\cdot bc\cdot\left(-ac\right)+\left(ac\right)^3-3\left(abc\right)^2=0\)
=>\(-a^3c^3+a^3c^3+3a^2b^2c^2-3a^2b^2c^2=0\)
=>0=0(đúng)

a) x 2 - 3 2 x + 9 16 . b) 9 t 2 + 6t + 1.
c) 1 9 − 9 a 2 d) a 4 – 4 a 2 + 4.

b: Ta có: \(N=a^3+b^3+3ab\)
\(=\left(a+b\right)^3-3ab\left(a+b\right)+3ab\)
\(=1-3ab+3ab\)
=1
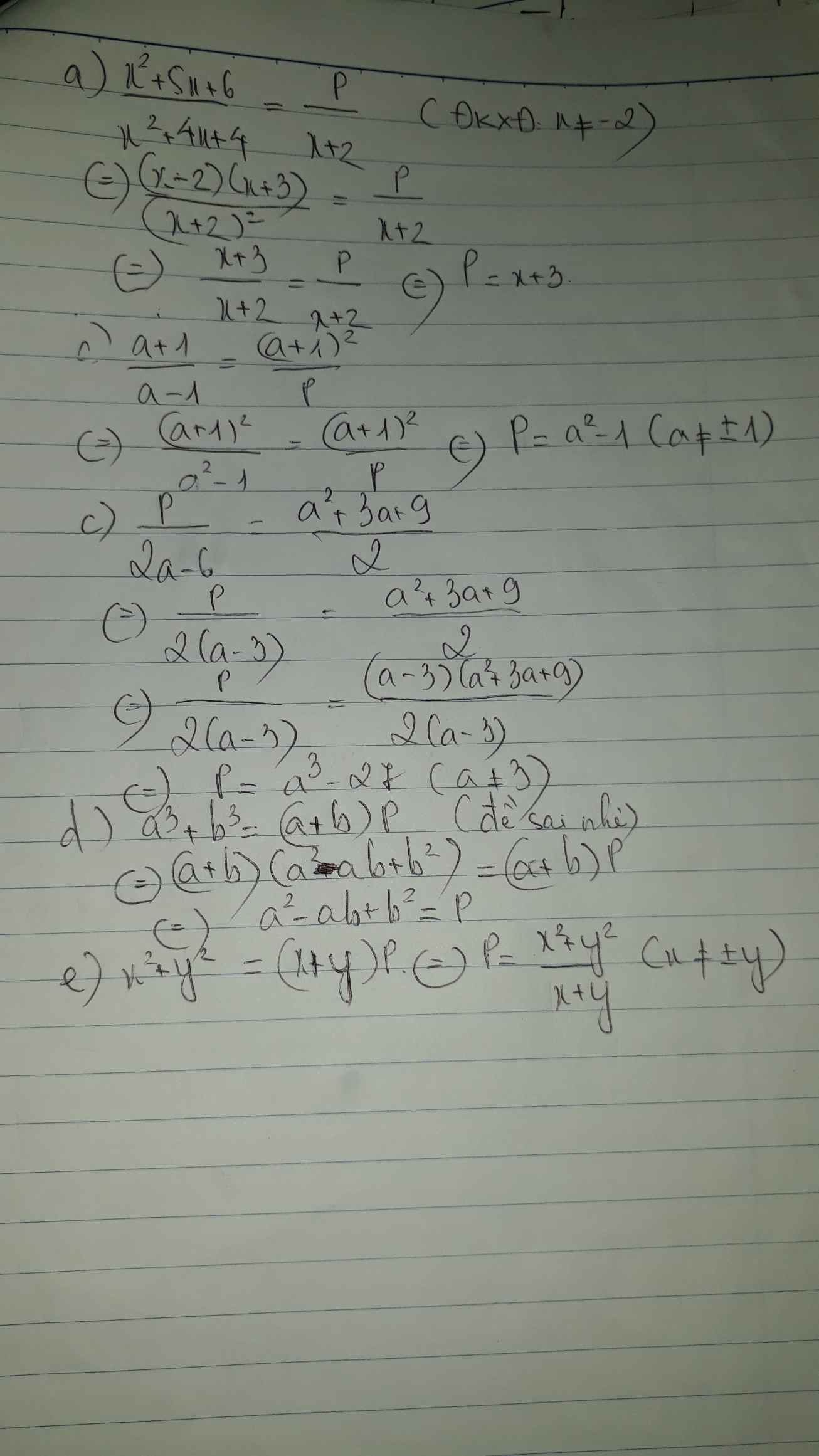
2.\(a^3+b^3=\left(a+b\right)^3-3ab\left(a+b\right)=1-3ab\)
1a)\(\left(3a+1\right)^2+\left(2-3a\right)\left(2+3a\right)=9a^2+6a+1+4-9a^2\)
.......................................................\(=6a+5\)