Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(=\dfrac{\left(x+1\right)^2}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{x+1}{x^2-x+1}\)

\(ĐK:5\left(x-2\right)^2\ne0\Leftrightarrow x-2\ne0\Leftrightarrow x\ne2\)

Đề này còn có lý, lần sau chú ý đọc kĩ đề trước khi đăng lên, tránh làm mất thời gian vô ích:
\(\left|x-2y\right|\le\dfrac{1}{\sqrt{x}}\Rightarrow1\ge\sqrt{x}\left|x-2y\right|\Rightarrow1\ge x\left(x-2y\right)^2\)
\(\Rightarrow1\ge x^3-4x^2y+4xy^2\)
Tương tự: \(\dfrac{1}{\sqrt{y}}\ge\left|y-2x\right|\Rightarrow1\ge y^3-4xy^2+4xy^2\)
Cộng vế:
\(\Rightarrow2\ge x^3+y^3=\dfrac{1}{2}\left(x^3+x^3+1\right)+\left(y^3+1+1\right)-\dfrac{5}{2}\ge\dfrac{1}{2}.3x^2+3y-\dfrac{3}{2}=\dfrac{3}{2}\left(x^2+2y\right)-\dfrac{5}{2}\)
\(\Rightarrow\dfrac{3}{2}\left(x^2+2y\right)\le\dfrac{9}{2}\Rightarrow x^2+2y\le3\)

\(b\) hữu hạn nên \(x^2+ax+2=0\) có nghiệm \(x=1\)
\(\Rightarrow1+a+2=0\Rightarrow a=-3\)
\(\lim\limits_{x\rightarrow1}\dfrac{\sqrt{x}-1}{x^2-3x+2}=\lim\limits_{x\rightarrow1}\dfrac{x-1}{\left(x-1\right)\left(x-2\right)\left(\sqrt{x}+1\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{1}{\left(x-2\right)\left(\sqrt{x}+1\right)}=-\dfrac{1}{2}\Rightarrow b=-\dfrac{1}{2}\)
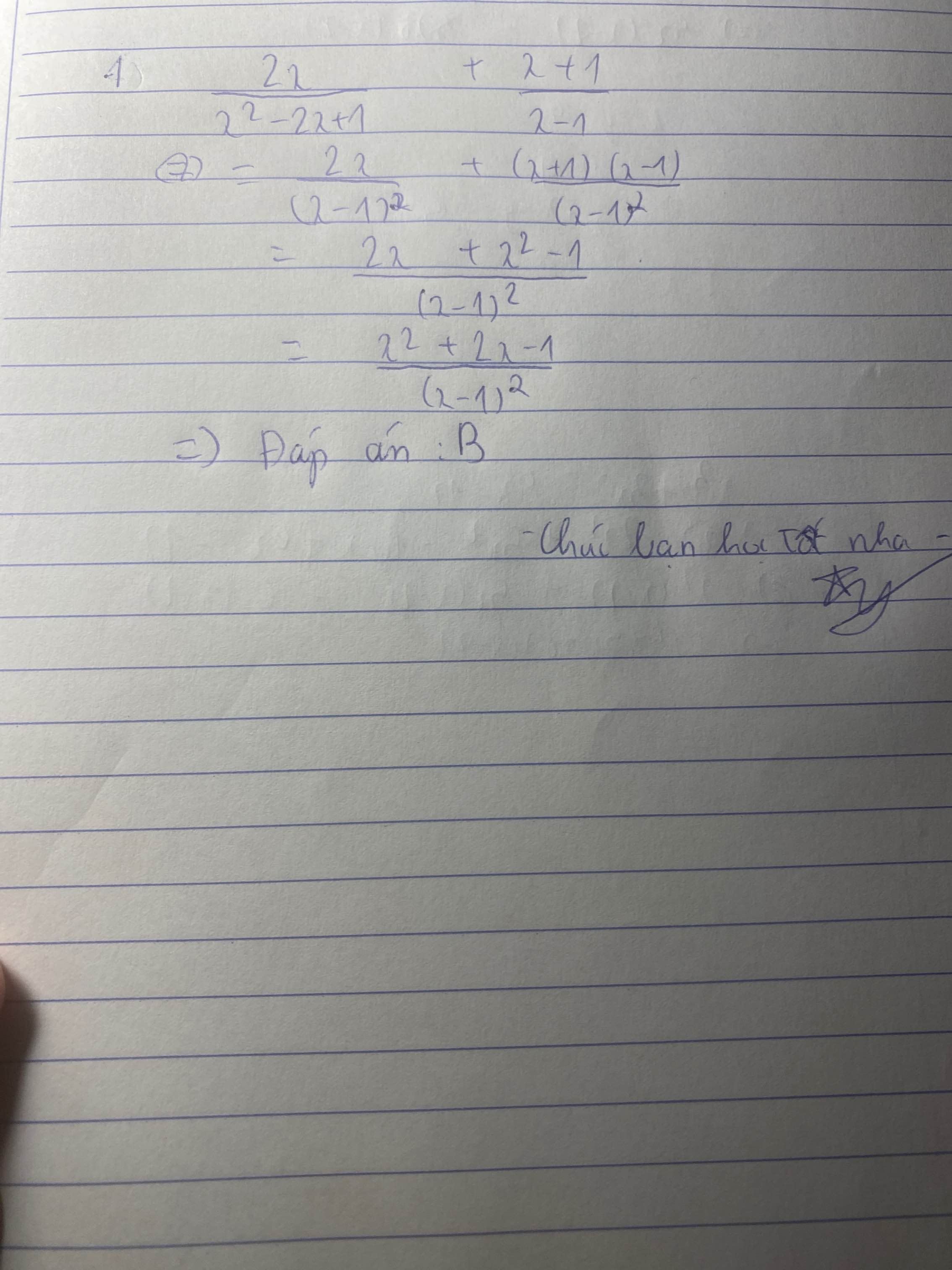
\(\dfrac{1}{x-1}=\dfrac{x+1}{\left(x-1\right)\left(x+1\right)};\dfrac{2}{x+1}=\dfrac{2\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\)