Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



câu 2 có lẽ dễ nhất luôn :
tách x^2+(1+y)^2=1 thành x^2+1+2y+y^2=1 (1)
tách y^2+(1+x)^2=1 thành y^2+1+2x+x^2=1 (2)
lấy(1) trừ( 2)
==>>>> x=y
tự làm tiếp nhé

a)\(\hept{\begin{cases}x+y+xy=11\\x^2y+xy^2=30\end{cases}}\Leftrightarrow\hept{\begin{cases}x+y+xy=11\\xy\left(x+y\right)=30\end{cases}}\)
Đặt \(S=x+y;P=xy\left(S^2\ge4P\right)\) có:
\(\hept{\begin{cases}S+P=11\\SP=30\end{cases}}\Rightarrow\hept{\begin{cases}S=5\\P=6\end{cases}}or\hept{\begin{cases}S=6\\P=5\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x+y=6\\xy=5\end{cases}or\hept{\begin{cases}x+y=5\\xy=6\end{cases}}}\)
\(\Rightarrow\hept{\begin{cases}x=1\\y=5\end{cases};\hept{\begin{cases}x=5\\y=1\end{cases}}or\hept{\begin{cases}x=2\\y=3\end{cases}};\hept{\begin{cases}x=3\\y=2\end{cases}}}\)
b)Thay số hay đặt ẩn.... gì đó tùy, nhiều pp
ra \(x=8;y=-8\)


Ta có: \(\hept{\begin{cases}x^2+xy+y=1\\x+xy+y^2=1\end{cases}}\)
\(\Leftrightarrow x^2+xy+y+x+xy+y^2=2\)
\(\Leftrightarrow\left(x^2+2xy+y^2\right)+\left(x+y\right)=2\)
\(\Leftrightarrow\left(x+y\right)^2+\left(x+y\right)=2\)
\(\Leftrightarrow\left(x+y\right)\left(x+y+1\right)=2\)
Sau đó xét các TH
\(hpt< =>\hept{\begin{cases}\left(x+y\right)^2+\left(x+y\right)=2\\x^2-y^2-\left(x-y\right)=0\end{cases}}< =>\hept{\begin{cases}\left(x+y\right)^2+\left(x+y\right)=2\\\left(x+y\right)\left(x-y\right)-\left(x-y\right)=0\end{cases}}\)
Đặt \(\left\{x+y;x-y\right\}\rightarrow\left\{a;b\right\}\)Suy ra \(\hept{\begin{cases}a^2+a-2=0\\ab-b=0\end{cases}< =>\hept{\begin{cases}a^2+a-2=0\\b\left(a-1\right)=0\end{cases}< =>\hept{\begin{cases}b=0\\a=1\end{cases}}}}\)
\(< =>\hept{\begin{cases}x+y=1\\x-y=0\end{cases}< =>\hept{\begin{cases}x=1-y\\1-y-y=0\end{cases}< =>\hept{\begin{cases}x=1-y\\y=\frac{1}{2}\end{cases}}< =>x=y=\frac{1}{2}}}\)
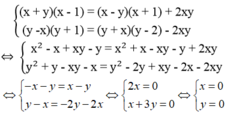
\(\left\{{}\begin{matrix}\left(x-1\right)\left(y+1\right)=xy-1\\\left(x-2\right)\left(y-2\right)=xy-8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}xy+x-y-1=xy-1\\xy-2x-2y+4=xy-8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-y=0\\-2x-2y=-12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-2y=0\\2x+2y=12\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x=12\\x-y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=x=3\end{matrix}\right.\)
\(\left\{{}\begin{matrix}\left(x-1\right)\left(y+1\right)=xy-1\\\left(x-2\right)\left(y-2\right)=xy-8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy+x-y-1=xy-1\\xy-2x-2y+4=xy-8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-y=0\\x+y=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=3\end{matrix}\right.\)