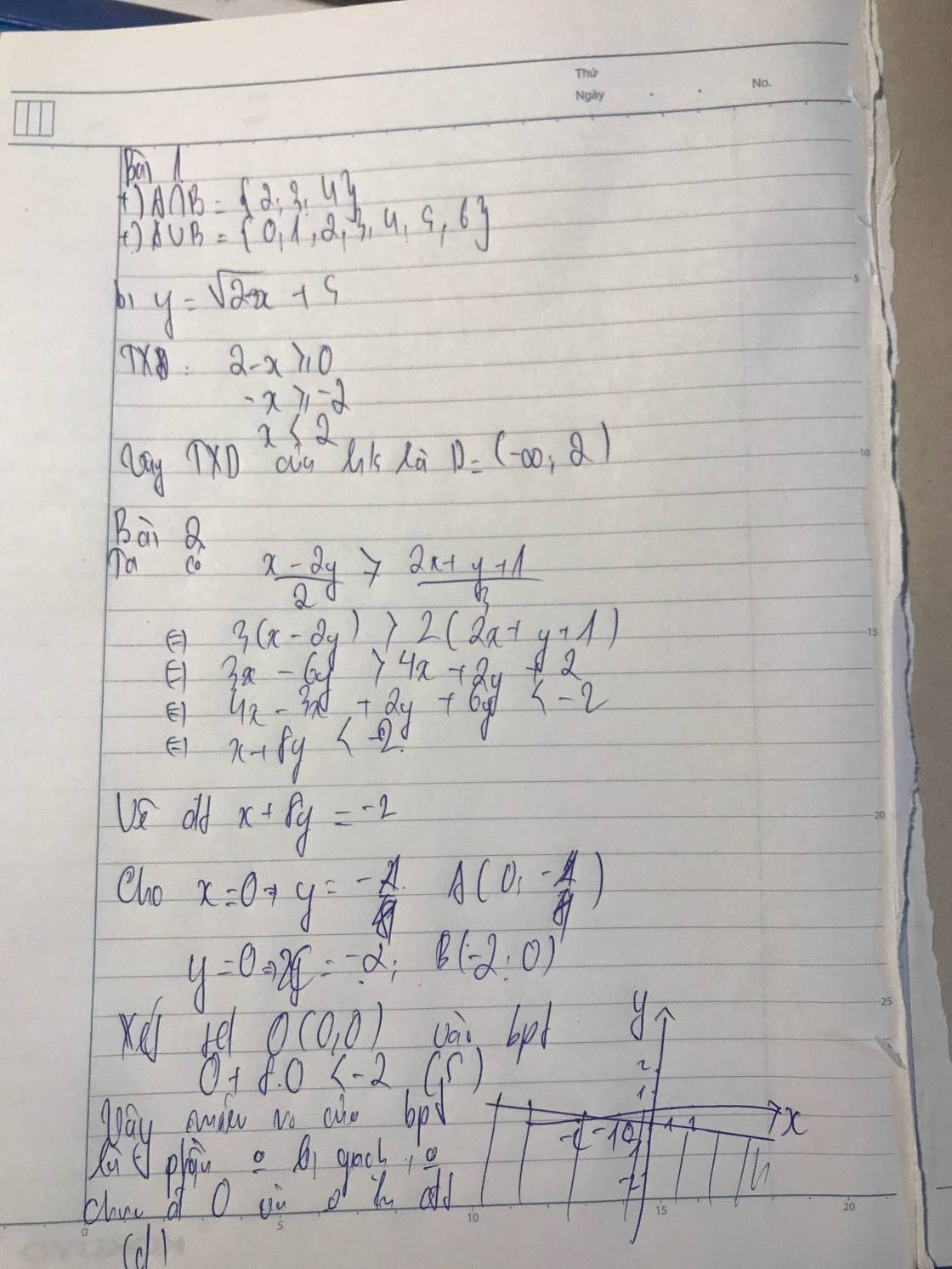Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(A\cap B=\left\{2;3;4\right\}\\ A\cup B=\left\{0;1;2;3;4;5;6\right\}\)
b) Để hàm số xđ thì : \(2-x\ge0< =>-x\ge-2< =>x\le2\)

1.
\(\left|mx-3\right|=mx-3\Leftrightarrow mx-3\ge0\)
\(\Leftrightarrow mx\ge3\)
\(x^2-4=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\) \(\Rightarrow B=\left\{-2;2\right\}\)
\(B\backslash A=B\Leftrightarrow A\cap B=\varnothing\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2m< 3\\2m< 3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>-\frac{3}{2}\\m< \frac{3}{2}\end{matrix}\right.\)
\(\Rightarrow-\frac{3}{2}< m< \frac{3}{2}\)
2.
\(A=\left(-\infty;-3\right)\cup\left(\sqrt{6};+\infty\right)\)
À thôi nhìn tập \(C_RB\) thấy kì kì
Đề là \(\left(-5;2\right)\cup\left(\sqrt{3};\sqrt{11}\right)\) hay \(\left(-5;-2\right)\cup\left(\sqrt{3};\sqrt{11}\right)\) vậy bạn?
Vì đề như bạn ghi thì \(2>\sqrt{3}\) nên \(\left(-5;2\right)\cup\left(\sqrt{3};\sqrt{11}\right)=\left(-5;\sqrt{11}\right)\) luôn còn gì, người ta ghi dạng hợp 2 khoảng làm gì nữa?
Đề là (-5;2) \(\cup\) (\(\sqrt{3}\); \(\sqrt{11}\)) đó bạn!

Hàm số xác định trên R khi và chỉ khi:
a.
\(\left(2m-4\right)x+m^2-9=0\) vô nghiệm
\(\Leftrightarrow\left\{{}\begin{matrix}2m-4=0\\m^2-9\ne0\end{matrix}\right.\) \(\Rightarrow m=2\)
b.
\(x^2-2\left(m-3\right)x+9=0\) vô nghiệm
\(\Leftrightarrow\Delta'=\left(m-3\right)^2-9< 0\)
\(\Leftrightarrow m^2-6m< 0\Rightarrow0< m< 6\)
c.
\(x^2+6x+2m-3>0\) với mọi x
\(\Leftrightarrow\Delta'=9-\left(2m-3\right)< 0\)
\(\Leftrightarrow m>6\)
e.
\(-x^2+6x+2m-3>0\) với mọi x
Mà \(a=-1< 0\Rightarrow\) không tồn tại m thỏa mãn
f.
\(x^2+2\left(m-1\right)x+2m-2>0\) với mọi x
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(2m-2\right)=m^2-4m+3< 0\)
\(\Leftrightarrow1< m< 3\)

a.
\(\Leftrightarrow x^2+2\left(m-1\right)x+m^2+3m+5\ne0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m^2+3m+5\right)< 0\)
\(\Leftrightarrow-5m-4< 0\)
\(\Leftrightarrow m>-\dfrac{4}{5}\)
b.
\(\Leftrightarrow x^2+2\left(m-1\right)x+m^2+m-6\ge0\) ;\(\forall x\)
\(\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m^2+m-6\right)\le0\)
\(\Leftrightarrow-3m+7\le0\)
\(\Rightarrow m\ge\dfrac{7}{3}\)
c.
\(x^2-2\left(m+3\right)x+m+9>0\) ;\(\forall x\)
\(\Leftrightarrow\Delta'=\left(m+3\right)^2-\left(m+9\right)< 0\)
\(\Leftrightarrow m^2+5m< 0\Rightarrow-5< m< 0\)