Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Gọi \(I\left(x;y\right)\) là tâm đường tròn ngoại tiếp \(\Delta ABC\)
\(\Rightarrow\left\{{}\begin{matrix}IA=IB\\IA=IC\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}IA^2=IB^2\\IA^2=IC^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(-3-x\right)^2+\left(6-y\right)^2=\left(1-x\right)^2+\left(-2-y\right)^2\\\left(-3-x\right)^2+\left(6-y\right)^2=\left(6-x\right)^2+\left(3-y\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2y=-5\\3x-y=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)

\(AH=\dfrac{2S_{ABC}}{BC}=2\sqrt{5}\)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{5}\)
\(\Rightarrow BH=\dfrac{1}{3}BC\)
\(\Rightarrow\left[{}\begin{matrix}\overrightarrow{BH}=\dfrac{1}{3}\overrightarrow{BC}\\\overrightarrow{BH}=-\dfrac{1}{3}\overrightarrow{BC}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}H\left(1;1\right)\\H\left(3;-3\right)\end{matrix}\right.\) (sử dụng công thức điểm chia đoạn thẳng theo tỉ lệ)

Đáp án B
![]() => Đường thẳng AB có pt là: x- y – 5= 0.
=> Đường thẳng AB có pt là: x- y – 5= 0.
Gọi G(a;3a- 8) suy ra C( 3a- 5; 9a -19).
Ta có:

Vậy C( 1 ; -1) và C( -2 ; 10)

a: G thuộc Oy nên G(0;y)
\(GA=\sqrt{\left(-3-0\right)^2+\left(0-y\right)^2}=\sqrt{y^2+9}\)
\(GC=\sqrt{\left(4-0\right)^2+\left(1-y\right)^2}=\sqrt{y^2-2y+1+16}\)
Để GA=GC thì y^2-2y+17=y^2+9
=>-2y=-8
=>y=4
b: \(HA=\sqrt{\left(-3-x\right)^2+\left(0-y\right)^2}=\sqrt{\left(x+3\right)^2+y^2}\)
\(HC=\sqrt{\left(4-x\right)^2+\left(1-y\right)^2}\)
HA=HC
=>(x+3)^2+y^2=(x-4)^2+(y-1)^2
=>x^2+y^2+6x+9=x^2-8x+16+y^2-2y+1
=>6x+9=-8x+16-2y+1
=>6x+9=-8x-2y+17
=>14x+2y-8=0
=>7x+y-4=0

Đáp án A
Giả sử A( x0 ; y0) , Do A ; B đối xứng nhau qua Ox nên B( x0 ; -y0).
Ta có:
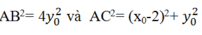
Vì A thuộc (E) nên:
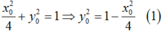
Vì AB = AC nên:
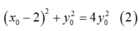
Thay (1) vào (2) ta được:
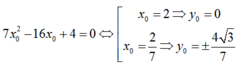
Vì điểm A khác C và Acó tung độ dương nên:
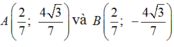

Bài 2:
a: Xét ΔOHA vuông tại A và ΔOHB vuông tại B có
OH chung
\(\widehat{AOH}=\widehat{BOH}\)
Do đó: ΔOHA=ΔOHB
Suy ra: HA=HB
hay ΔHAB cân tại H
b: Xét ΔOAB có
OH là đường cao
AD là đường cao
OH cắt AD tại C
Do đó: C là trực tâm của ΔOAB
Suy ra: BC\(\perp\)Ox
c: \(\widehat{HOA}=\dfrac{60^0}{2}=30^0\)
Xét ΔOHA vuông tại A có
\(\cos HOA=\dfrac{OA}{OH}\)
\(\Leftrightarrow OA=\dfrac{\sqrt{3}}{2}\cdot4=2\sqrt{3}\left(cm\right)\)

\(\overrightarrow{BC}=\left(-5;-15\right)=-5\left(1;3\right)\)
Đường thẳng AH vuông góc BC nên nhận \(\left(1;3\right)\) là 1 vtpt
Phương trình AH:
\(1\left(x-0\right)+3\left(y-3\right)=0\Leftrightarrow x+3y-9=0\)
A là giao điểm AH và denta nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}x+3y-9=0\\5x-7y-1=0\end{matrix}\right.\) \(\Rightarrow A\left(3;2\right)\)
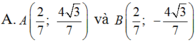
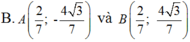
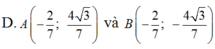
Câu 1: Chưa đủ dữ kiện để làm. Bạn xem lại đề.
Câu 2: Gọi tọa độ điểm H(a,b)
Ta có: \(\overrightarrow{AH}=(a-3; b-2); \overrightarrow{BC}=(1;8); \overrightarrow{BH}=(a-4; b+1); \overrightarrow{AC}=(2; 5)\)
Vì H là trực tâm tam giác ABC nên:
\(\left\{\begin{matrix} \overrightarrow{AH}.\overrightarrow{BC}=0\\ \overrightarrow{BH}.\overrightarrow{AC}=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a-3+8(b-2)=0\\ 2(a-4)+5(b+1)=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} a+8b=19\\ 2a+5b=3\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=\frac{-71}{11}\\ b=\frac{35}{11}\end{matrix}\right.\)