Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E F G H I K N M Q P
a) - Xét tứ giác AMCI , có :
+ AM // CI ( GT )
+ AM = CI ( GT )
=> AMCI là hình bình hành ( 2 cạnh đối song song và bằng nhau )
=> AI // MC hay EH // FG (1)
- XÉt tứ giác BNDK có :
+ BN // DK ( GT )
+ BN = DK ( GT : N , K lần lượt là trung điểm BC , DA và BC = DA )
=> BNDK là hình bình hành ( 2 cạnh đối song song và bằng nhau )
=> BK // DN hay EF // HG ( 2)
- Từ 1 và 2 ta có : EFGH là hình bình hành ( các cặp cạnh đối song song )
- Kẻ FQ vuông góc AI tai Q
=> \(S_{EFGH\:}=FQ.EH\)
- Mặt khác : \(S_{AMCI}=FQ.AI\)( Vì MC // AI nên FQ là đường cao chung )
=> \(\frac{S_{EFGH\:}}{S_{AMCI}}=\frac{FQ.EH}{FQ.AI}=\frac{EH}{AI}\)(3)
- LẠi có :
+ Xét tam giác AHD có : KE // DH và K là trung điểm của AD nên => E là trung điểm của AH hay AE = EH
+ Xét tam giác DCG có : HI // CG , I là trung điểm của DC nên => H là trung diểm của DG => HI là đường trung bình của tam giác DCG => \(HI=\frac{1}{2}.CG\)mà CG = FG = EH nên \(HI=\frac{1}{2}.EH\)
=> \(AI=AE+EH+HI=2.EH+\frac{1}{2}.EH=\frac{5.EH}{2}\)
Thay vào 3 , ta được :
\(\frac{S_{EFGH\:}}{S_{AMCI}}=\frac{EH}{AI}=EH:\frac{5.EH}{2}=\frac{2.EH}{5.EH}=\frac{2}{5}\)
b) - Kẻ AP vuông góc với CD tại Q
- Ta có : \(S_{ABCD}=AP.CD\)và \(S_{AMCI}=AP.CI\)
=> \(\frac{S_{AMCI}}{S_{ABCD}}=\frac{AP.CI}{AP.CD}=\frac{CI}{CD}=\frac{1}{2}\Rightarrow S_{AMCI}=\frac{1}{2}.S_{ABCD}\)
Từ ý a , ta có : \(S_{EFGH\:}=\frac{2}{5}.SAMCI=\frac{2}{5}.\frac{1}{2}.S_{ABCD}=\frac{1}{5}.S_{ABCD}\)
MÀ ABCD có diện tích là S nên \(S_{EFGH\:}=\frac{1}{5}.S\)

1:
Xet ΔOAE và ΔOCF có
góc OAE=góc OCF
góc AOE=góc COF
=>ΔOAE đồng dạng với ΔOCF
=>AE/CF=OE/OF
Xét ΔOEB và ΔOFD có
góc OEB=góc OFD
góc EOB=góc FOD
=>ΔOEB đồng dạng với ΔOFD
=>EB/FD=OE/OF=AE/CF
mà CF=DF
nên EB=AE
=>E là trung điểm của BA

b tham khảo nha
a) Do ABCD là hình bình hành nên AB= CD và AB//CD
Và E và F là trung điểm của AB và CD => AE=BE=CF=DF và BE//DF
Xét tứ giác DEBF có : BE//DF và BE=DF=> DEBF là hình bình hành
b)
Xét AEDF có AE//DF và AE=DF=> AEDF là hình bình hành
Lại có: CD= 2BC= 2 AD nên AD= AE (=1/2 CD)
=> hình bình hành AEDF là hình thoi
c)ta cm được AECF là hình bình hành và M, N là trung điểm của AF và CE
=> MF= EN và MF//EN=> EMFN là hình bình hành
Lại có AEDF là hình thoi nên AN⊥DE tại M
=> góc EMF vuông=> hình bình hành EMFN là hình chữ nhật
d) Chứng minh được
SAFB=12SABCDSBEC=14SABCDˆB=600⇒ΔBECdeucanh=AB2=2(cm)⇒SBEC=√3(cm2)⇒SAFB

Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD

GIÚP MÌNH ĐI! GẤP LĂM! SÁNG 9/12/2018 LÀ MÌNH PHẢI NỘP RỒI.
A B C D M N I K E N P a) MN là dường trung bình tam giác ABD,PE là đường trung bình tam giác ACD=>MN//AD,PQ//AD=>PE//MN.
tương tự, ta có: NQ//MP. ==>MNQP laf hbh.
b) IP là đường trung bình tam giác ADC=>IP //CD, KN là đường trung bình tam giác BDC=>KN //CD, IK là đường trung bình hình thang ABCD=>IK //CD .==>NP // CD(theo tiên đề ơ-clit).
còn câu c bạn cố gắng nha, khuya quá mẹ mk bắt ngủ nên ko ghi rõ ra, phần đường trung bình là do có các trung điểm đã cho. thông cảm nha

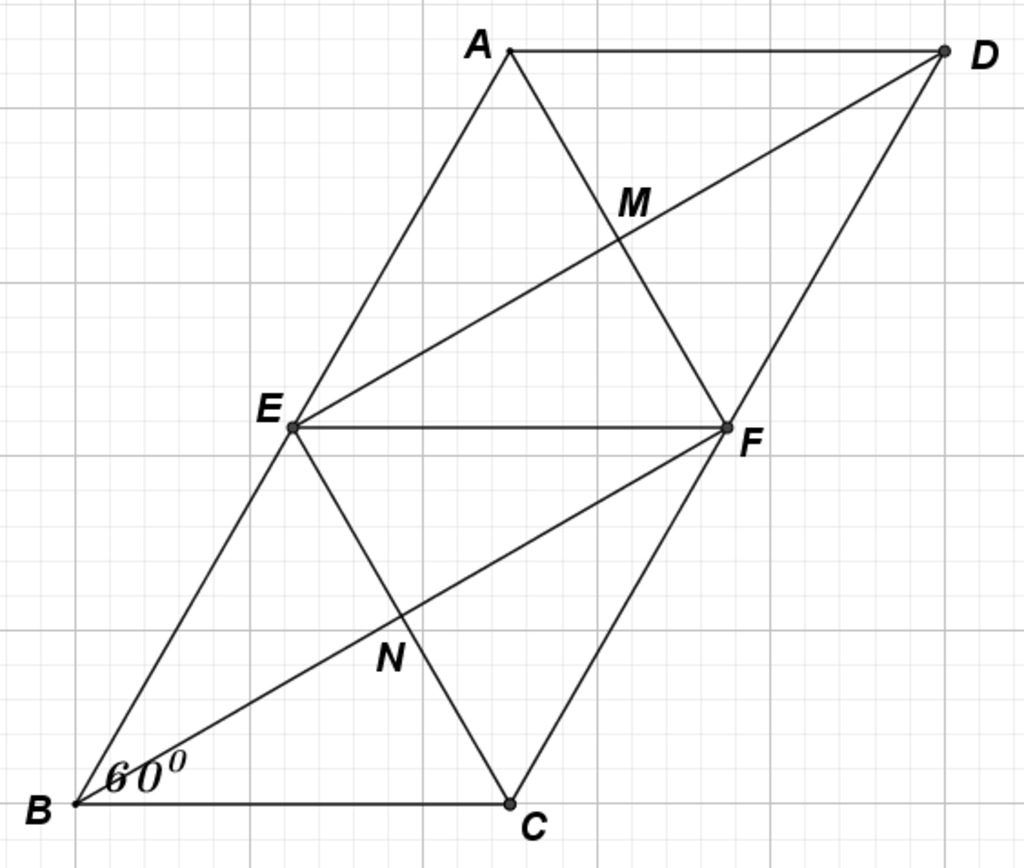
Bài 1:
a: Xét tứ giác ABEF có
BE//AF
BE=AF
BE=BA
Do đó: ABEF là hình thoi
b: Xét ΔBIE có BI=BE
nên ΔBIE cân tại B
mà góc IBE=60 độ
nên ΔBIE đều
=>góc I=60 độ
Xét tứ giác AFEI có
EF//AI
góc I=góc A
Do đó AFEI là hình thang cân
c: Xét ΔBAD có
BF là đường trung tuyến
BF=AD/2
Do đó: ΔBAD vuông tại B
=>DB vuông góc với BI
Xét tứ giác BICD có
BI//CD
BI=CD
Do đó: BICD là hình bình hành
mà DB vuông góc với BI
nên BICD là hình chữ nhật
d: Xét ΔAED có
EF la trung tuyến
FE=DA/2
Do đó: ΔAED vuông tại E
=>góc AED=90 độ