Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A D E I B C M N
a) Xét \(\Delta ABD\) và \(\Delta ACE\) ,có :
AD = AE ( Tam giác ADE cân tại A )
\(\widehat{ADE}=\widehat{AED}\) ( Tam giác ADE cân tại A )
BD = CE ( gt )
=> \(\Delta ABD=\Delta ACE\left(c.g.c\right)\)
=> AB = AC
=> \(\Delta ABC\) cân tại A
b) Xét \(\Delta BMD\) và \(\Delta CNE\) ,có :
BD = CE ( gt )
\(\widehat{BMD}=\widehat{CNE}=90^0\)
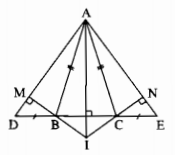
a) Xét ∆ADE cân tại A nên góc D = góc E
Xét ∆ABD và ∆ACE, ta có:
AD = AE (gt)
góc D = góc E (chứng minh trên)
DB = EC (gt)
Suy ra: ∆ABD = ∆ACE (c.g.c)
Suy ra: AB = AC (hai cạnh tương ứng)
Vậy ∆ABC cân tại A.
b) Xét hai tam giác vuông BMD và CNE, ta có:
góc BMD=góc CNE=90o
BD = CE (gt)
góc D = góc E (chứng minh trên)
Suy ra: ∆BMD = ∆CNE (cạnh huyền, góc nhọn)
Suy ra: BM = CN (hai cạnh tương ứng)
c) Ta có: ∆BMD = ∆CNE (chứng minh trên)
Suy ra: góc DBM=góc ECN (hai góc tương ứng)
góc DBM=góc IBC (đối đỉnh)
góc ECN = góc ICB (đối đỉnh)
Suy ra: góc IBC=góc ICB hay ∆IBC cân tại I.
d) Xét ∆ABI và ∆ACI, ta có:
AB = AC (chứng minh trên)
IB = IC (vì ∆IBC cân tại I)
AI cạnh chung
Suy ra: ∆ABI = ∆ACI (c.c.c) ⇒ góc BAI=góc CAI (hai góc tương ứng)
Vậy AI là tia phân giác của góc BAC

A B C D E 60
a) Xét ΔADE và ΔACE có:
AB = AC (gt)
Góc A là góc chung
BD = CE (gt)
=> ΔADE = ΔACE ( c-g-c)
=> AD = AE (2 cạnh tương ứng)
b) Vì góc ADE=60°
=> Góc ADE = 180° - góc ADB = 180° - góc AEC = góc AED
=> Góc ADE = góc AED = 60°
Mà góc ADE + AED = 60° + 60° => Góc DAE = 180° - 120° = 60°
Vậy ΔADE là tam giác cân
Nguyễn Lê Hoàng ViệtNguyễn Huy ThắngNguyễn Huy TúTrần Việt Linh

a: Xét ΔAED và ΔCEF có
EA=EC
\(\widehat{AED}=\widehat{CEF}\)
ED=EF
Do đó:ΔAED=ΔCEF
Ta có:ΔAED=ΔCEF
nên \(\widehat{DAE}=\widehat{FCE}\)
b: Xét tứ giác ADCF có
E là trung điểm của AC
E là trung điểm của DF
Do đó: ADCF là hình bình hành
SUy ra: AD//CF
c: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của AC
Do đó: DE là đường trung bình
=>DE=1/2BC

a )
Xét : \(\Delta ABHva\Delta ADH,co:\)
\(\widehat{H_1}=\widehat{H_2}=90^o\left(gt\right)\)
BH = HD ( gt )
AH là cạnh chung
Do do : \(\Delta ABH=\Delta ADH\left(c-g-c\right)\)
b )
Ta có : \(\Delta ABD\) là tam giác đều ( cmt )
= > \(\widehat{BAD}=60^o\) ( trong tam giác đều mỗi góc bằng 60o )
Ta có : \(\widehat{CAD}=\widehat{BAC}-\widehat{BAD}=90^o-60^o=30^o\) ( tia AD nằm giữa 2 tia AB và AC )
Hay : \(\widehat{EAD}=30^o\left(E\in AC\right)\)
Ta có :\(\widehat{ADH}=60^o\) ( \(\Delta ABD\) là tam giác đều )
Ta có : \(\widehat{HAD}=\widehat{H_2}-\widehat{ADH}=90^o-60^o=30^o\)
Ta có : \(AH\perp BC\) và \(ED\perp BC\)
= > \(AH//ED\) ( vì cùng vuông góc với BC )
=> \(\widehat{HAD}=\widehat{ADE}=30^o\) ( 2 góc so le trong của AH//ED )
=> \(\Delta AED\) là tam giác cân , và cân tại E ( vì có 2 góc ở đáy bằng nhau ( \(\widehat{HAD}=\widehat{ADE}=30^o\)) )
c ) mình không biết chứng minh AH = HF = FC nha , mình chỉ chứng minh \(\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{AH^2}\) thôi nha :
Ta có : \(\Delta ABC\) vuông tại A và AH là đường cao ( gt )
= > \(\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{AH^2}\) ( hệ thức lượng trong tam giác vuông )
Hình mình vẽ hơi xấu , thông cảm nha
HỌC TỐT !!!
a) Tam giác ABC có AH là đường cao đồng thời là trung tuyến ( BH=HD)
\(\rightarrow\) tam giác ABD cân tại A
Mà \(\widehat{B}\) = 60 độ \(\rightarrow\) tam giác ABD đều
b) Tam giác ABD đều nên \(\widehat{ADB}\) = \(\widehat{BAD}\) = 60 độ
\(\rightarrow\) \(\widehat{ADE}\) = \(\widehat{HDE}\) - \(\widehat{ADB}\) = 30 độ
Tương tự có \(\widehat{DAE}\) = 30độ
\(\Rightarrow\) Tam giác ADE cân tại E
c1) Xét tam giác AHC và tam giác CFA
\(\widehat{ACF}\) = \(\widehat{CAF}\) = 30độ
AC chung
\(\rightarrow\) tam giác bằng nhau ( cạnh huyền - góc nhọn)
\(\rightarrow\) AH = FC
Ta có \(\widehat{BAD}\) = 60 độ và \(\widehat{BAH}\) = 30 độ
\(\rightarrow \) \(\widehat{HAD}\) = 30 độ hay \(\widehat{HAF}\) = 30 độ
____Phần còn lại cm tam giác HAF cân là ra
Mk bận chút việc nên ms làm đến đây thui nka ~
Bài 1: Đặt \(\frac{a}{b}=\frac{c}{d}=k\)\(\Rightarrow\left\{\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
\(VT=\frac{a+5b}{c+5d}=\frac{bk+5b}{dk+5d}=\frac{b\left(k+5\right)}{d\left(k+5\right)}=\frac{b}{d}\left(1\right)\)
\(VP=\frac{bk-b}{dk-d}=\frac{b\left(k-1\right)}{d\left(k-1\right)}=\frac{b}{d}\left(2\right)\)
Từ (1) và (2) ta có điều phải chứng minh
Tự vẽ hình
a) Chứng minh AD = AE.
Vì \(\Delta\)ABC cân tại A
=> AB = AC và \(\widehat{ABC}\) = \(\widehat{ACB}\)
hay \(\widehat{ABD}\) = \(\widehat{ACE}\)
Xét \(\Delta\)ABD và \(\Delta\)ACE có:
AB = AC (c/m trên)
\(\widehat{ABD}\) = \(\widehat{ACE}\) (c/m trên)
BD = CE (gt)
=> \(\Delta\)ABD = \(\Delta\)ACE (c.g.c)
=> AD = AE (2 cạnh t/ư)
b) Có nhận xét gì về các góc của tam giác ADE , nếu biết góc ADE = 60 độ.
BL:
Do AD = AE nên \(\Delta\)ADE cân tại A
=> \(\widehat{ADE}\) = \(\widehat{AED}\) = 60o
Áp dụng tc tổng 3 góc trong 1 tg ta có:
\(\widehat{ADE}\) + \(\widehat{AED}\) + \(\widehat{DAE}\) = 180o
=> 1200 + \(\widehat{DAE}\) = 180o
=> \(\widehat{DAE}\) = 60o