Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

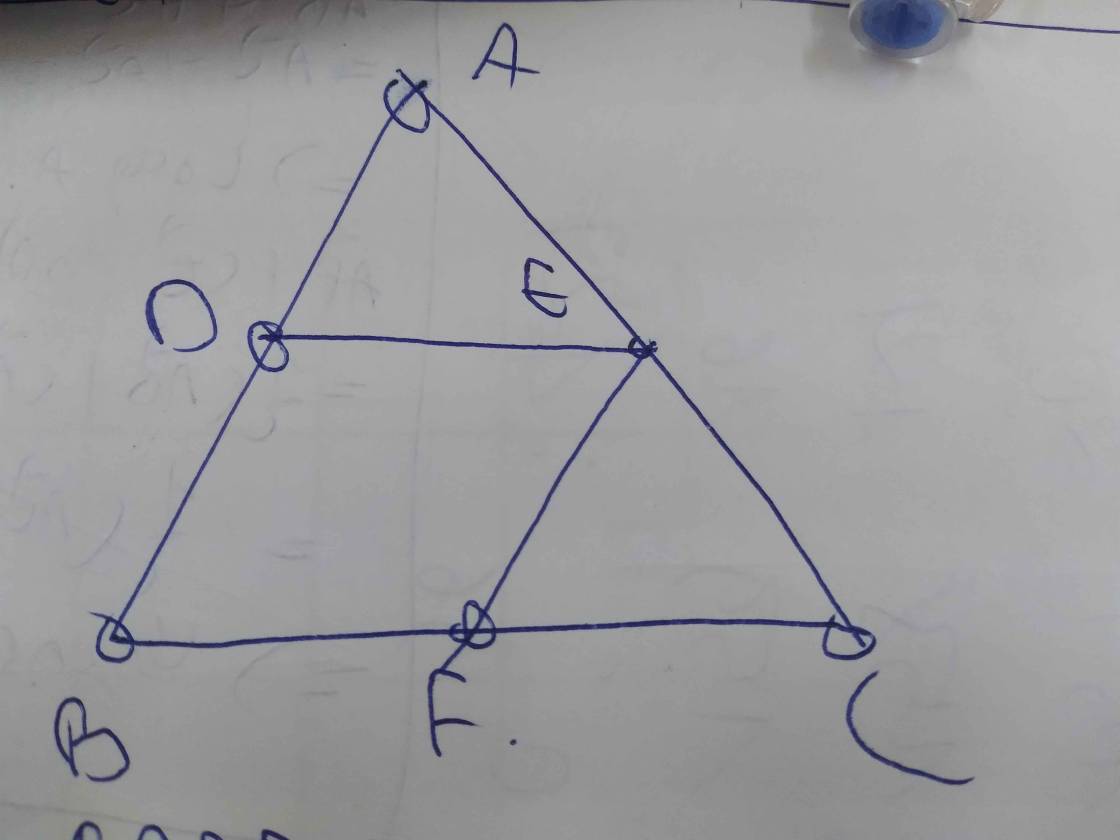
a, vì BD song song với AC nên góc B2 bằng góc C2. tương tự được góc C1 bằng góc B1.Do đó tam giác ABC = tam giác BAE(g.c.g) (dpcm)
b, vì AC song song với BD nên góc D bằng góc ACF.
vì AF song song với BC nên góc C1= góc CAF = B2.
theo câu a, tam giác ABC= tam giác DCB nên AC=BD, AB=DC
Do đó tam giác BDC=tam giác ACF(g.c.g) nên DC = CF=AB nên DF= DC+CF=2.AB.
Tương tự ta đc; DE=2.AC, EF=2.BC
Do đó Chu vi tam giác DEF bằng 2 lần chu vi tam giác ABC và bằng 30 cm

Gọi Bx là tia đối của tia BA. Lấy E trên AC sao cho AB = AE
Xét tam giác BAD=EAD c-g-c => BD = DE và DEC = CBx
Trong tam giác ABC, BAC + ABC + ACB = 180 => ACB = 180 - BAC - ABC => ACB < 180 - ABC
Ta có DBx + ABC = 180 (hai góc kề bù) => DBx = 180 - ABC
=>ACB < DBx => ACB < DEC => Trong tam giác DEC, DC > DE (Quan hệ giữa góc và cạnh)
Vậy BD < DC

a: Xét ΔABC và ΔCDA có
\(\widehat{BAC}=\widehat{DCA}\)
AC chung
\(\widehat{ACB}=\widehat{CAD}\)
Do đó: ΔABC=ΔCDA
b: Xét ΔADB và ΔCBD có
BD chung
AD=CB
AB=CD
Do đó: ΔADB=ΔCBD

a, xét \(\Delta\)ABC và \(\Delta\)ADC có
AC chung
\(\widehat{A1}=\widehat{C2}\) ( AD // BC )
\(\widehat{C1}=\widehat{A2}\) ( AB // DC )
=> \(\Delta\)ABC =\(\Delta\)ADC (g.c.g)
b, xét \(\Delta\) ADB và \(\Delta CBD\) có
BD chung
\(\widehat{B1}=\widehat{D2}\) ( AB // DC )
\(\widehat{D1}=\widehat{B2}\)( AD // BC )
=> \(\Delta CBD\) = \(\Delta\)ADB ( g.c.g )
c, xét \(\Delta ABO\) và \(\Delta COD\) có
\(\widehat{C1}=\widehat{A2}\) ( AB // DC )
AB = DC ( \(\Delta\)ABC =\(\Delta\)ADC ) \(\widehat{B1}=\widehat{D2}\) ( AB // DC ) => \(\Delta ABO\) = \(\Delta COD\) ( g.c.g )