Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có :
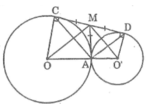
MO là tia phân giác của góc (CMA) (tính chất hai tiếp tuyến cắt nhau)
MO’ là tia phân giác của góc (DMA) (tính chất hai tiếp tuyến cắt nhau)
Suy ra : MO ⊥ MO’ (tính chất hai góc kề bù)
Tam giác MOO’ vuông tại M có MA ⊥ OO’ (tính chất tiếp tuyến)
Theo hệ thức lượng trong tam giác vuông, ta có :
M A 2 = OA.O’A = 4,5.2 = 9 ⇒ MA = 3 (cm)
Mà MA = 12 CD ⇒ CD = 2.MA = 2.3 = 6 (cm)

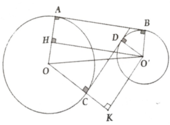
Kẻ O’H ⊥ OA; O’K ⊥ OC
OH = 4; OK = 8
Đặt CD = x => AB = 2x
O O ' 2 = 64 + x 2
và O O ' 2 = 16 + 4 x 2
=> x = 4 => OO' = 80 cm

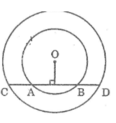
Kẻ OI ⊥ AB. Ta có: OI ⊥ CD
Trong đường tròn (O) (nhỏ) ta có : OI ⊥ AB
Suy ra :
IA = IB (đường kính vuông góc dây cung) (1)
Trong đường tròn (O) (lớn) ta có : OI ⊥ CD
Suy ra :
IC = ID (đường kính vuông góc dây cung)
Hay IA + AC = IB + BD (2)
Từ (1) và (2) suy ra: AC = BD.

