TD
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 7 2023
=>2x-3căn x+2căn x-3>0
=>(2căn x-3)(căn x+1)>0
=>2căn x-3>0
=>x>9/4
KN
2
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
30 tháng 10 2023
\(\Leftrightarrow x^2-4x+3>0\left(x\ne\pm5\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x< 1\\x>3\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
30 tháng 10 2023
Lời giải:
ĐK: $25-x^2>0\Leftrightarrow -5< x< 5$
$\frac{x^2-4x+3}{\sqrt{25-x^2}}>0$
$\Leftrightarrow x^2-4x+3>0$ (do $\sqrt{25-x^2}>0$)
$\Leftrightarrow (x-1)(x-3)>0$
$\Leftrightarrow x>3$ hoặc $x<1$
Kết hợp với đkxđ suy ra $3< x< 5$ hoặc $-5< x< 1$
TP
2
21 tháng 1 2022
b) (0,5 - x)2 - 3 = 0 ⇔ 0,52 + x2 - 2.0,5x - 3 = 0
⇔ x2 + 0,25 - x - 3 = 0
⇔ x2 - x - 2,75 = 0
⇔ ????
21 tháng 1 2022
c: \(\Leftrightarrow\left(2x-3\sqrt{2}\right)\left(2x+\sqrt{2}\right)=0\)
hay \(x\in\left\{\dfrac{3\sqrt{2}}{2};-\dfrac{\sqrt{2}}{2}\right\}\)
Z
0
NT
1
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 2 2021
ĐKXĐ: \(x\le2\)
Xét trên miền xác định:
\(\Leftrightarrow\dfrac{2x^3+3x}{7-2x}-1+1-\sqrt{2-x}>0\)
\(\Leftrightarrow\dfrac{\left(x-1\right)\left(2x^2+2x+7\right)}{7-2x}+\dfrac{x-1}{1+\sqrt{2-x}}>0\)
\(\Leftrightarrow\left(x-1\right)\left(\dfrac{2x^2+2x+7}{7-2x}+\dfrac{1}{1+\sqrt{2-x}}\right)>0\)
\(\Leftrightarrow1< x\le2\)
5 tháng 9 2023
a: ĐKXĐ: x>=3
Sửa đề: \(\sqrt{4x-12}-\sqrt{9x-27}+\sqrt{\dfrac{25x-75}{4}}-3=0\)
=>\(2\sqrt{x-3}-3\sqrt{x-3}+\dfrac{5}{2}\sqrt{x-3}-3=0\)
=>\(\dfrac{3}{2}\sqrt{x-3}=3\)
=>\(\sqrt{x-3}=2\)
=>x-3=4
=>x=7(nhận)
b: ĐKXĐ: x>=0
\(\dfrac{\sqrt{x}-2}{\sqrt{x}+1}< =-\dfrac{3}{4}\)
=>\(\dfrac{\sqrt{x}-2}{\sqrt{x}+1}+\dfrac{3}{4}< =0\)
=>\(\dfrac{4\sqrt{x}-8+3\sqrt{x}+3}{4\left(\sqrt{x}+1\right)}< =0\)
=>\(7\sqrt{x}-5< =0\)
=>\(\sqrt{x}< =\dfrac{5}{7}\)
=>0<=x<=25/49
c: ĐKXĐ: x>=5
\(\sqrt{9x-45}-14\sqrt{\dfrac{x-5}{49}}+\dfrac{1}{4}\sqrt{4x-20}=3\)
=>\(3\sqrt{x-5}-14\cdot\dfrac{\sqrt{x-5}}{7}+\dfrac{1}{4}\cdot2\cdot\sqrt{x-5}=3\)
=>\(\dfrac{3}{2}\sqrt{x-5}=3\)
=>\(\sqrt{x-5}=2\)
=>x-5=4
=>x=9(nhận)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 8 2021
ĐKXĐ: \(x\ge0\)
\(\dfrac{x}{\sqrt{x}-1}>0\Leftrightarrow\left\{{}\begin{matrix}x\ne0\\\sqrt{x}-1>0\end{matrix}\right.\)
\(\Leftrightarrow x>1\)
NL
1
2 tháng 12 2017
ĐK : \(\orbr{\begin{cases}x>0\\x< -1\end{cases}}\)
Đặt \(\sqrt{\frac{x+1}{x}}=t>0\)
\(bpt\Leftrightarrow\frac{1}{t^2}-2t>3\Leftrightarrow2t^3+3t^2-1< 0\Leftrightarrow\left(2t-1\right)\left(t+1\right)^2< 0\Leftrightarrow2t-1< 0\)(do \(\left(t+1\right)^2>0\))
\(\Leftrightarrow t< \frac{1}{2}hay\sqrt{\frac{x+1}{x}}< \frac{1}{2}\Rightarrow\frac{x+1}{x}< \frac{1}{4}\)
Với x >0, ta có: \(\frac{x+1}{x}< \frac{1}{4}\Leftrightarrow4\left(x+1\right)< 1\Leftrightarrow x< -\frac{3}{4}\left(trái.với.gt:x>0\right)\)
Với x<-1 ta có: \(\frac{x+1}{x}< \frac{1}{4}\Rightarrow4\left(x+1\right)>x\Rightarrow x>-\frac{3}{4}\Rightarrow-\frac{3}{4}< x< -1\)
Vậy nghiệm của hệ phương trình là: \(-\frac{3}{4}< x< -1\)
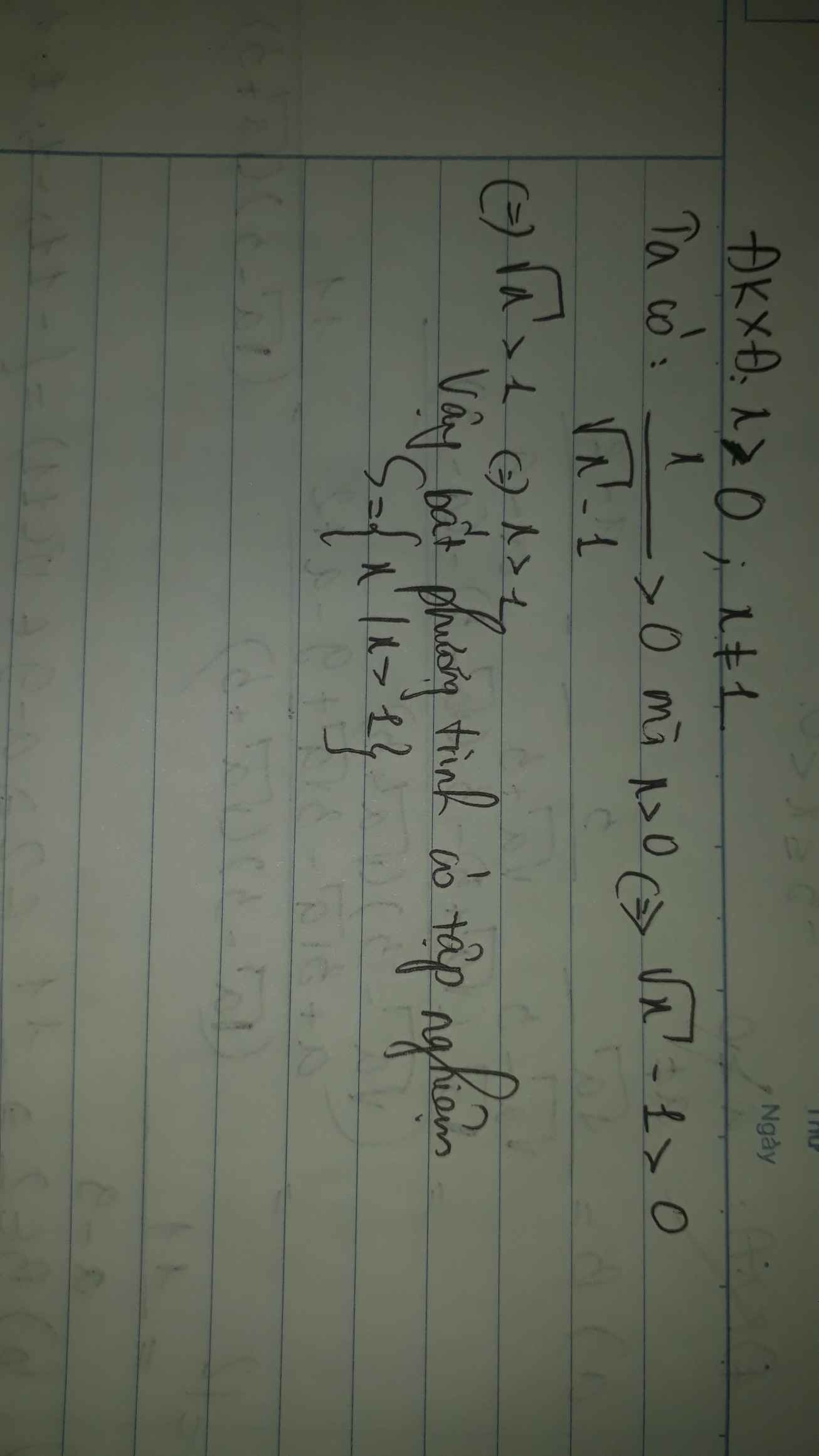
Đk: \(x\ge0\)
Đặt \(t=\sqrt{x}\Rightarrow t\ge0\)
\(\Rightarrow t^2-3t+2< 0\) (1)
\(\Rightarrow\left(1\right)\Leftrightarrow\left[{}\begin{matrix}t< 1\\t>2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}\sqrt{x}< 1\\\sqrt{x}>2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x< 1\\x>4\end{matrix}\right.\)
Kết hợp đk \(x\ge0\Rightarrow BPT\Leftrightarrow\left[{}\begin{matrix}0\le x< 1\\x>4\end{matrix}\right.\)