Cho đường tròn tâm O bán kính R. Một đường thẳng d không đi qua O và cắt đường tròn tại hai điểm phân biệt A và B. Trên d lấy điểm M sao cho A nằm giữa M và B. Từ M kẻ hai tiếp tuyến MC và MD với đường tròn (C, D là các tiếp điểm).
1.Chứng minh rằng 4 điểm M,C,O,D cùng nằm trên một đường tròn.
2. Gọi I là trung điểm của AB. Đường thẳng IO cắt tia MD tại K.
Chứng minh rằng KD. KM = KO. KI
3. Một đường thẳng đi qua O và song song với CD cắt các tia MC và MD lần lượt tại E và F. Xác định vị trí của M trên d sao cho diện tích tam giác MEF đạt giá trị nhỏ nhất.

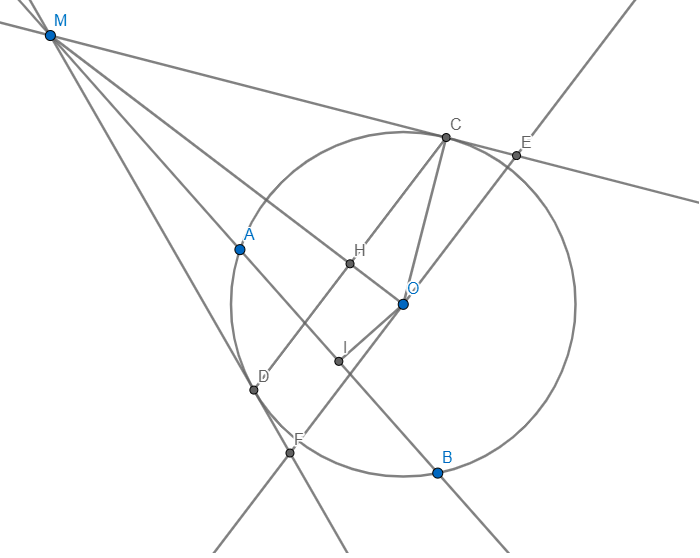
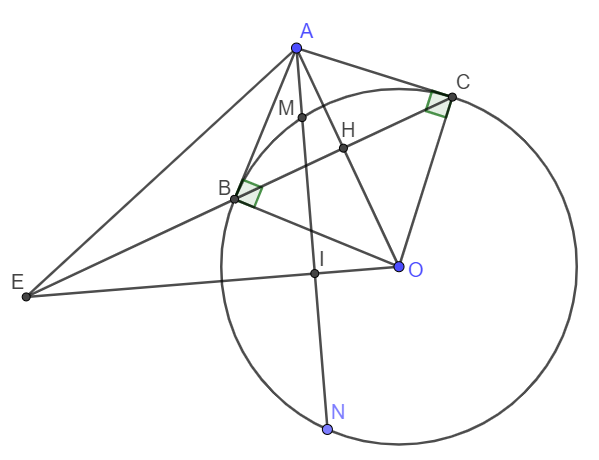
1. MCOD nội tiếp đường tròn (+2 góc đối nhau =180o)
=> đpcm
2. OAI = OBI (c.g.c)
=> ^AOI = ^BOI
=> OI là phân giác cx là trung tuyến
=> OI là đường cao
=> ^OIA = 90o
=> ^OIM = 90o
OIDM nội tiếp (OIM =ODM = 90o)
=> KOD = KMI
.................=> tg KMI ~ tg KOD
=> đpcm....
Im mồm 🤬🤬🤬