Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4) Ta có: \(AM//PQ\)( cùng vuông góc với OC )
Xét tam giác COQ có: \(EM//OQ\)
\(\Rightarrow\frac{CE}{CO}=\frac{EM}{OQ}\)( hệ quả của định lý Ta-let ) (1)
Xét tam giác COP có: \(AE//OP\)
\(\Rightarrow\frac{CE}{CO}=\frac{AE}{OP}\)( hệ quả của định lý Ta-let ) (2)
Từ (1) và (2) \(\Rightarrow\frac{EM}{OQ}=\frac{AE}{OP}\)Mà AE=EM
\(\Rightarrow OQ=OP\)
Xét tam giác CPQ và tam giác COP có chung đường cao hạ từ C, đáy \(OP=\frac{PQ}{2}\)
\(\Rightarrow S_{\Delta CPQ}=2.S_{\Delta COP}\)
Ta có: \(S_{\Delta COP}=\frac{1}{2}OA.CP=\frac{1}{2}R.CP\)
Áp dụng hệ thức lượng trong tam giác COP vuông tại O có đường cao OA ta có:
\(OA^2=CA.AP\)
Mà \(CA.AP\le\frac{\left(CA+AP\right)^2}{4}=\frac{PC^2}{4}\)( BĐT cô-si )
Dấu "=" xảy ra \(\Leftrightarrow AC=AP\)
\(\Rightarrow PC^2\ge4OA^2\)
\(\Rightarrow PC\ge2OA=2R\)
\(\Rightarrow S_{\Delta COP}\ge R^2\)
\(\Rightarrow S_{\Delta CPQ}\ge2R^2\)
Dấu "=" xảy ra \(\Leftrightarrow AC=AP\)
Mà tam giác COP vuông tại O có đường cao OA
\(\Rightarrow AC=AP=OA=R\)
Khi đó áp dụng định lý Py-ta-go vào tam giác CAO vuông tại A ta được:
\(AC^2+AO^2=OC^2\)
\(\Rightarrow OC=\sqrt{AC^2+AO^2}=R\sqrt{2}\)
Vậy điểm C thuộc đường thẳng d sao cho \(OC=R\sqrt{2}\)thì diện tích tam giác CPQ nhỏ nhất

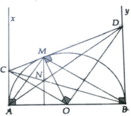
a, Từ CA, CM là tiếp tuyến của (O) chứng minh được A,C,M,O ∈ đường tròn bán kính O C 2
b, Chứng minh OC,BM cùng vuông góc với AM . từ đó suy ra OC//BM
c, S A C D B = A C + B D A B 2 = A D . A B 2
=> S A C D B nhỏ nhất khi CD có độ dài nhỏ nhất
Hay M nằm chính giữa cung AB
d, Từ tính chất hai giao tuyến => AC = CM và BM=MD, kết hợp với AC//BD
ta chứng minh được C N N B = C M M D => MN//BD => MN ⊥ AB
a: Xét tứ giác CMON có \(\widehat{CMO}+\widehat{CNO}=90^0+90^0=180^0\)
nên CMON là tứ giác nội tiếp
=>C,M,O,N cùng thuộc một đường tròn
b: Xét (O) có
\(\widehat{CMA}\) là góc tạo bởi tiếp tuyến MC và dây cung MA
\(\widehat{ABM}\) là góc nội tiếp chắn cung AM
Do đó: \(\widehat{CMA}=\widehat{ABM}=\widehat{CBM}\)
Xét ΔCMA và ΔCBM có
\(\widehat{CMA}=\widehat{CBM}\)
\(\widehat{MCA}\) chung
Do đó: ΔCMA~ΔCBM
=>\(\dfrac{CM}{CB}=\dfrac{CA}{CM}\)
=>\(CM^2=CA\cdot CB\)
c: Xét (O) có
CM,CN là các tiếp tuyến
Do đó: CM=CN
=>C nằm trên đường trung trực của MN(1)
Ta có: OM=ON
=>O nằm trên đường trung trực của MN(2)
Từ (1),(2) suy ra OC là đường trung trực của MN
=>OC\(\perp\)MN tại H
Xét ΔCMO vuông tại M có MH là đường cao
nên \(CH\cdot CO=CM^2\)
=>\(CH\cdot CO=CA\cdot CB\)
=>\(\dfrac{CH}{CB}=\dfrac{CA}{CO}\)
Xét ΔCHA và ΔCBO có
\(\dfrac{CH}{CB}=\dfrac{CA}{CO}\)
\(\widehat{HCA}\) chung
Do đó: ΔCHA~ΔCBO
=>\(\widehat{CHA}=\widehat{CBO}\)
mà \(\widehat{CBO}=\widehat{OAB}\)(ΔOAB cân tại O)
nên \(\widehat{CHA}=\widehat{OAB}\)