
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Với 3 số 3, cách làm rất đơn giản: 3 x 3 - 3 = 6.
Sử dụng phép 6 + 6 - 6 = 6 đối với 3 số 6.
Đối với 3 số 4, ta có thể sử dụng phép căn bậc hai từng số rồi tính tổng của chúng.
Với 3 số 9, ta sử dụng phép căn bậc hai của 9 thành 3 rồi tính như trong trường hợp 3 số 3.
Cách làm đối với 3 số 5 và 3 số 7 tương tự nhau:
5 + 5 : 5 = 6
7 - 7 : 7 = 6
3 số 8 là trường hợp dễ gây nhầm lẫn nhất vì nhiều người sẽ sử dụng phép căn bậc ba của 8 bằng 2 rồi tính tổng của chúng. Tuy nhiên, người ra đề quy định, người giải không được thêm bất kỳ số tự nhiên nào trong khi ký hiệu căn bậc ba có số 3.
Trong trường hợp này, Ty Yann dùng hai lần căn bậc hai của 8 + 8 (tương đương căn bậc 4 của 16) bằng 2. Sau đó, ông dùng phép tính 8 - 2 = 6.
Với 3 số 1, tác giả dùng phép giai thừa:
(1 + 1 + 1)! = 3! = 3 x 2 x 1 = 6.

Cũng đơn giản thôi. 10x9x8x7: (6+5+4)x3x2x1=2016
Thử lại nhé!

Chọn đáp án C.
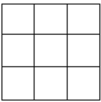
Số cách sắp xếp 9 chữ số đã cho vào ô vuông bằng n(Ω)=9!
Ta có: A là biến cố: “tồn tại một hàng hoặc một cột gồm ba số chẵn”.
Do có 4 số chẵn (2, 4, 6, 8) nên A là biến cố: “có đúng một hàng hoặc một cột gồm 3 số chẵn”.
Ta tính n A :
Chọn 4 ô điền số chẵn:
Ø Chọn một hàng hoặc một cột thì có 6 cách.
Ø Chọn một ô còn lại có 6 cách.
Điền 4 số chẵn vào 4 ô trên có 4! cách.
Điền 5 số lẻ vào 5 ô còn lại có 5! Cách.
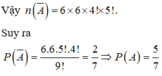

a, Ta thấy với a,b >0 thì \(\frac{a}{b}<\frac{a+n}{b+n}\), với a,b<0 thì \(\frac{a}{b}>\frac{a+\left(-n\right)}{b+\left(-n\right)}\) \(\left(n\in Z;\right)n>0\)
Vậy ta sắp xếp như sau:
\(-\frac{8}{9};-\frac{6}{7};-\frac{4}{5};-\frac{1}{2};\frac{2}{3};\frac{3}{4};\frac{5}{6};\frac{7}{8};\frac{9}{10}\)
b, Có:
\(\frac{0}{23}=0\)
\(-\frac{14}{5}<-1<\frac{-15}{19}<-\frac{15+\left(-2\right)}{19+\left(-2\right)}=-\frac{13}{17}\)
\(\frac{5}{2}>\frac{4}{2}=2>\frac{11}{7}=\frac{99}{63}>\frac{13}{9}=\frac{91}{63}\)
Vậy ta sắp xếp như sau:
\(-\frac{14}{5};-\frac{15}{19};-\frac{13}{17};0;\frac{13}{9};\frac{11}{7};\frac{5}{2}\)

Chọn đáp án B
Phương pháp
Chia các TH sau:
TH1: a<b<c.
TH2: a=b<c.
TH3: a<b=c.
TH4: a=b=c.
Cách giải
Gọi số tự nhiên có 3 chữ số là a b c ¯ (0≤a,b,c≤9, a≠0).
=> S có 9.10.10=900 phần tử. Chọn ngẫu nhiên một số từ S => n(Ω)=900
Gọi A là biến cố: “Số được chọn thỏa mãn a≤b≤c”.
TH1: a<b<c. Chọn 3 số trong 9 số từ 1 đến 9, có duy nhất một cách xếp chúng theo thứ tự tăng dần từ trái qua phải nên TH này có C 9 3 số thỏa mãn.
TH2: a=b<c, có C 9 2 số thỏa mãn.
TH3: a<b=c có C 9 2 số thỏa mãn.
TH4: a=b=c có 9 số thỏa mãn.
⇒ n ( A ) = C 9 3 + 2 C 9 2 + 9 = 165
Vậy P ( A ) = 11 60 .


8\(\frac{1}{14}\)-6\(\frac{3}{7}\)
C1:8\(\frac{1}{14}\)-6\(\frac{6}{14}\)
=2\(\frac{-5}{14}\)
Ta có hỗn số này : 8\(\frac{1}{3}\)-\(6\frac{3}{7}\)
C1:\(\frac{25}{3}\)-\(\frac{45}{7}\)
=\(\frac{175}{21}\)-\(\frac{135}{21}\)
=\(\frac{40}{21}\)=\(1\frac{19}{21}\)