Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\omega=\frac{2\pi}{T}=2\pi\)(rad/s)
Vận tốc cực đại \(v_{max}=\omega A=2\pi.5=10\pi\)(cm/s)
Vì vận tốc là đại lượng biến thiên điều hòa theo thời gian, nên ta khảo sát nó bằng véc tơ quay.
10π v 5π M N -10π O
Tại thời điểm t, trạng thái của vận tốc ứng với véc tơ OM, sau 1/6 s = 1/6 T, véc tơ quay: 1/6.360 = 600
Khi đó, trạng thái của vận tốc ứng với véc tơ ON --> Vận tốc đạt giá trị cực đại là: \(10\pi\) (cm/s)
Đáp án B.

\(\lambda = v/f = 80/20 = 4cm.\)
\(\triangle \varphi = \pi-0=\pi.\)
Nhận xét: \(BM-AM=(BI+IM)-(AI-IM)=2MI\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{BM-AM}{\lambda}-\frac{\triangle\varphi}{2\pi})|\\=|2a\cos\pi(\frac{2MI}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{6}{4}-\frac{\pi}{2\pi})| = |-2a|=2a=10 mm.\)

- Điểm cách nguồn (1/4)λ:
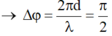
⇒ 2 điểm dao động vuông pha nhau.
- Phương trình của O là:
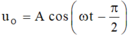
- Phương trình tại điểm M là:
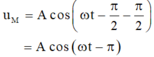
- Tại T/2 thì:
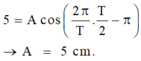

+ Điểm cách nguồn 1 4 λ → ∆ φ = 2 π d λ = π 2 → 2 điểm dao động vuông pha nhau.
+ Phương trình của O là: u o = A cos ( ω t - π 2 )
+ Phương trình tại điểm M là: u M = A cos ( ω t - π 2 - π 2 ) = A cos ( ω t - π )
+ Tại t = T 2 thì: 5 = Acos ( 2 π T . T 2 - π ) → A = 5 cm.
Đáp án D


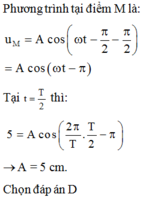
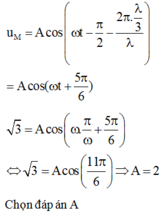
Đáp án C
+ Độ lệch pha giữa O và điểm M đang xét
∆ φ = ∆ φ x + ∆ φ t = 2 π ∆ x λ + ω ∆ t = 2 π
=> điểm đang xét cùng pha với O.
=> (uO)t=0 = A = (uM)0,5T = 5 cm.