Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án cần chọn là: C
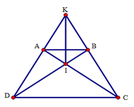
Xét tam giác ACD và tam giác BDC có:
+ AD = BC (do ABCD là hình thang cân)
+ AC = BD (do ABCD là hình thang cân)
+ CD là cạnh chung
Suy ra ΔACD = ΔBDC (c.c.c)
Suy ra A C D ^ = B D C ^ (hai góc tương ứng), suy ra tam giác ICD cân tại I.
Nên C sai vì ta chưa đủ điều kiện để IC = CD
Tam giác KCD có hai góc ở đáy bằng nhau nên tam giác KCD cân ở K nên B đúng.
Xét tam giác KDI và tam giác KCI có:
+ KD = KC (do ΔKCD cân tại K))
+ KI là cạnh chung
+ IC = ID
Suy ra ΔKDI = ΔKCI (c.c.c)
Suy ra K D I ^ = C K I ^ , do đó KI là phân giác A K B ^ nên D đúng.
Ta có AB // CD (do ABCD là hình thang) nên K A B ^ = K C D ^ ; K B A ^ = K C D ^ (các cặp góc đồng vị bằng nhau)
Mà K D C ^ = K C D ^ (tính chất hình thang cân) nên K A B ^ = K C D ^ (tính chất hình thang cân) nên hay ΔKAB cân tại K. Do đó A đúng

Đáp án cần chọn là: A
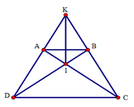
Xét tam giác ACD và tam giác BDC có:
+ AD = BC (do ABCD là hình thang cân)
+ AC = BD (do ABCD là hình thang cân)
+ CD là cạnh chung
Suy ra ΔACD = ΔBDC (c.c.c)
Suy ra A C D ^ = B D C ^ (cmt), suy ra tam giác ICD cân tại I. Do đó ID = IC (1)
Tam giác KCD có hai góc ở đáy bằng nhau nên tam giác KCD cân ở K.
Do đó KC = KD (2)
Từ (1) và (2) suy ra KI là đường trung trực của CD (*).
Xét tam giác ADB và tam giác BCA có:
+ AD = BC (cmt)
+ AB là cạnh chung
+ AC = BD
Suy ra ΔADB = ΔBCA (c.c.c)
Suy ra A B D ^ = B A C ^
Xét tam giác IAB có A B D ^ = B A C ^ nên tam giác IAB cân tại I.
Do đó IA = IB (3)
Ta có KA = KD – AD; KB = KC – BC
Mà KD = KC, AD = BC, do đó KA = KB (4)
Từ (3) và (4) suy ra KI là đường trung trực của AB. (**)
Từ (*) và (**) suy ra KI là đường trung trực của hai đáy (đpcm)

Em tham khảo câu 1 tại link dưới:
Câu hỏi của Thư Anh Nguyễn - Toán lớp 8 - Học toán với OnlineMath

Vì OE // DC ==> OA/AC = OE/DC (định lý Ta-let) (1)
Vì OF // DC ==> OB/BD = OF/DC (định lý Ta-let) (2)
Vì AB // CD ==> OA/OC = OB/OD (định lý ta-let)
Theo tính chất dãy tỉ số bằng nhau ta có:
OA/OC = OB/OD <=> OA / (OA + OC) = OB / (OB + OD)
<=> OA / AC = OB / BD (3)
Từ (1), (2) và (3) suy ra ta có:
OE / DC = OF / DC <=> OE = OF (đpcm)

A B E I C D H
Xét hình thang ABCD có
\(\widehat{C}=\widehat{D}=80^o\) => ABCD là hình thang cân => AD=BC
\(\Rightarrow\widehat{A}=180^o-\widehat{D}=180^o-80^o=100^o\) (Hai góc trong cùng phía)
Tương tự ta cũng có \(\widehat{B}=100^o\)
\(\Rightarrow\widehat{A}=\widehat{B}=100^o\)
Xét tg ABC và tg ABD có
AD=BC (cmt)
\(\widehat{A}=\widehat{B}\) (cmt)
AB chung
=> tg ABD = tg ABC (c.g.c) \(\Rightarrow\widehat{ADB}=\widehat{ACB}\)
Mà \(\widehat{ADB}+\widehat{BDC}=\widehat{ADC}=180^o=\widehat{BCD}=\widehat{ACB}+\widehat{ACD}\)
\(\Rightarrow\widehat{BDC}=\widehat{ACD}=\left(180^o-\widehat{CID}\right):2=60^o\)
=> tg CID là tg đều => CD=CI (1)
Xét tg ABI có
\(\widehat{BAC}=\widehat{ACD}=60^o\) (góc so le trong)
\(\widehat{ABD}=\widehat{BDC}=60^o\) (góc so le trong)
\(\widehat{AIB}=\widehat{CID}=60^o\) (góc đối đỉnh)
=> tg ABI là tg đều
Ta có AE là phân giác \(\widehat{BAI}\) (gt)
=> AE là đường trung trực, đường cao của tg ABI (trong tg đều đường phân giác đồng thời là đường cao, đường trung trực)
Xét tg BIE có
AE đồng thời là đường cao và đường trung trực => tg BIE cân tại E
\(\Rightarrow\widehat{DBC}=\widehat{BIE}\) (góc ở đáy tg cân)
Ta có
\(\widehat{DBC}=\widehat{B}-\widehat{ABD}=100^o-60^o=40^o=\widehat{BIE}\)
=> \(\widehat{BEI}=180^o-\left(\widehat{DBC}+\widehat{BIE}\right)=180^o-\left(40^o+40^o\right)=100^o\)
\(\Rightarrow\widehat{IEC}=180^o-\widehat{BEI}=180^o-100^o=80^o\)
Ta có
\(\widehat{BIC}=180^o-\widehat{CID}=180^o-60^o=120^o\)
\(\Rightarrow\widehat{EIC}=\widehat{BIC}-\widehat{BIE}=120^o-40^o=80^o\)
Xét tg CIE có
\(\widehat{IEC}=\widehat{EIC}=80^o\) => tg CIE cân tại C => CE=CI (2)
Từ (1) và (2) => CE=CD